Modeling and Analysis of Modern Fluid Problems

Liancun Zheng, Xinxin Zhang

• Publisher: Academic Press
• Year: 2017
• Print ISBN: 9780128117538
• eBook ISBN: 9780128117590
• Topic: Physical Sciences
• Subtopic: Fluid Mechanics

Modeling and Analysis of Modern Fluids helps researchers solve physical problems observed in fluid dynamics and related fields, such as heat and mass transfer, boundary layer phenomena, and numerical heat transfer. These problems are characterized by nonlinearity and large system dimensionality, and 'exact' solutions are impossible to provide using the conventional mixture of theoretical and analytical analysis with purely numerical methods.To solve these complex problems, this work provides a toolkit of established and novel methods drawn from the literature across nonlinear approximation theory. It covers Padé approximation theory, embedded-parameters perturbation, Adomian decomposition, homotopy analysis, modified differential transformation, fractal theory, fractional calculus, fractional differential equations, as well as classical numerical techniques for solving nonlinear partial differential equations. In addition, 3D modeling and analysis are also covered in-depth.- Systematically describes powerful approximation methods to solve nonlinear equations in fluid problems- Includes novel developments in fractional order differential equations with fractal theory applied to fluids- Features new methods, including Homotypy Approximation, embedded-parameter perturbation, and 3D models and analysis

Chapter 1

Introduction

L. Zheng and X. Zhang

Abstract

Nature is full of many nonlinear and random phenomena. The study of nonlinear phenomena is a matter of natural sciences, engineering, and even social economic problems. Many scientists and engineers spend a lot of time and effort to study mathematical modeling and solving methods for these problems. This chapter presents an introduction to modeling, the development of analytical methods for modern fluid problems, and the outline of this book.

Keywords

Adomian decomposition; Approximate solution; Differential transformation; Fractional viscoelastic fluid; Homotopy analysis; Nonlinear differential equations; Perturbation theory

1.1. Basic Ideals of Analytical Methods

1.1.1. Analytical Methods

Most problems in science and engineering are in essence nonlinear and can be modeled by nonlinear differential equations. However, because of the complexity of nonlinear differential equations, so far we have not found a suitable analytical method to arrive at general solutions for various nonlinear equations. For these nonlinear equations, most cannot be solved analytically and can be solved only by the approximate method. Many basic properties commonly used in linear equations, such as the superposition principle of solutions, are no longer held (Li, 1989; Wang, 1993; Zheng et al., 2003; Zheng and Zhang, 2013).

There is good progress in the development of approximate analytical methods to solve nonlinear partial/ordinary differential equations. Many approximate analytical methods have been proposed to solve nonlinear ordinary equations, partial equations, fractional differential equations (FDEs), and integral equations. The commonly used methods are perturbation, Adomian decomposition, homotopy analysis, variational iteration, and differential transformation. Based on those methods, this book presents some useful approaches to modeling and analytical methods for modern fluid problems.

To understand the essence of this book better, a short review of the concepts of Taylor series and Fourier series are presented here, which are the bases for exploring approximate analytical methods for solving nonlinear partial differential equations.

1.1.1.1. Taylor Series

Suppose f(x) ∈ Cⁿ[a,b], that f⁽ⁿ⁺¹⁾(x) exists on [a,b], x₀ ∈ [a,b]. For every x ∈ [a,b], there exists a number ξ = ξ(x) between x and x₀, such that

f(x)=Pn(x)+Rn(x),

(1.1)

where

Pn(x)=f(x0)+f′(x0)(x−x0)+⋯+f(n)(x0)n!(x−x0)n,

...

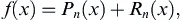
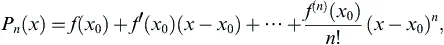
Table of contents

• Cover image
• Title page
• Table of Contents
• Copyright
• Preface
• Chapter 1. Introduction
• Chapter 2. Embedding-Parameters Perturbation Method
• Chapter 3. Adomian Decomposition Method
• Chapter 4. Homotopy Analytical Method
• Chapter 5. Differential Transform Method
• Chapter 6. Variational Iteration Method and Homotopy Perturbation Method
• Chapter 7. Exact Analytical Solutions for Fractional Viscoelastic Fluids
• Chapter 8. Numerical Methods
• Index