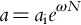Aircraft Sustainment and Repair

Rhys Jones, A.A. Baker, Neil Matthews, Victor K. Champagne, V K Champagne

• Publisher: Butterworth-Heinemann
• Year: 2017
• Print ISBN: 9780081005408
• eBook ISBN: 9780081005446
• Topic: Technology & Engineering
• Subtopic: Aeronautic & Astronautic Engineering
• Index: Technology & Engineering

Aircraft Sustainment and Repair is a one-stop-shop for practitioners and researchers in the field of aircraft sustainment, adhesively bonded aircraft joints, bonded composites repairs, and the application of cold spray to military and civil aircraft. Outlining the state-of-the-art in aircraft sustainment, this book covers the use of quantitative fractography to determine the in-service crack length versus flight hours curve, the effect of intergranular cracking on structural integrity and the structural significance of corrosion. The book additionally illustrates the potential of composite repairs and SPD applications to metallic airframes.- Covers corrosion damage assessment and management in aircraft structures- Includes a key chapter on U.S. developments in the emerging field of supersonic particle deposition (SPD)- Shows how to design and assess the potential benefits of both bonded composite repairs and SPD repairs to metallic aircraft structures to meet the damage tolerance requirements inherent in FAA ac 20-107b and the U.S. Joint Services

Chapter One

Rationale and Organisation

Rhys Jones^⁎; Neil Matthews^†; Alan A. Baker^‡,§; Victor Champagne, Jr.^{¶ ⁎} Monash University, Clayton, VIC, Australia
^† RUAG Australia, Bayswater, VIC, Australia
^‡ Advanced Composite Structures Australia, Melbourne, VIC, Australia
^§ Defence Science and Technology Group, Fairbairn, CBR, Australia
^¶ US Army Research Laboratory, Aberdeen, MD, United States

In general, the design of aerospace vehicles requires that all structures and repairs to load-bearing structural elements be designed in accordance with damage tolerance design principles, which are largely based on the discipline of fracture mechanics and which for military aircraft are detailed in the Joint Services Structural Guidelines-2006 (JSSG2006) [1] and in the USAF Damage Tolerant Design Handbook [2]. This design philosophy has evolved as a result of a number of high-profile (military aircraft) incidents some of which,¹ together with a number of civilian aircraft failures, are reviewed in Ref. [3]. As explained in Ref. [3]:

While there have been lessons learned from nearly all of the accidents and incidents, those that were seminal with respect to the design and certification of aircraft structures were the 1954 Comet failures, the 1958 B-47 accidents, the 1969 F-111 accident, the 1976 AVRO 748 accident, the 1978 Dan Air 707 Lusaka accident and the 1988 Aloha Boeing 737 accident. The Comet failures resulted in the use of fail-safe design in commercial aircraft; the B-47 accidents resulted in the development of the Air Force Aircraft Structural Integrity Programme (ASIP); the F-111 accident accelerated the introduction of damage tolerance design requirements in military aircraft; the AVRO 748 and Dan Air Boeing 707 accidents resulted in complementing commercial fail-safe design with damage tolerance requirements; and the Aloha Boeing 737 accident brought attention to the importance that WFD² has in limiting the safe operation of airplane structures.

The USAF [5] was one of the first to realise that the operational life of an aircraft was governed by the growth of small cracks and that the analysis tools needed for aircraft sustainment issues, that is, to assess in-service cracking, differed from those used in design. This conclusion was also one of the primary conclusions reached in the USAF-McDonnell Douglas (now Boeing) study into sustainment issues associated with cracking in the F-15 aircraft [6] and is also enunciated in Refs. [7,8]. It also led to the USAF developing a probabilistic approach to assessing the fatigue life of operational aircraft [5] in which crack growth was represented as an exponential function, viz.:

$a=a_{\mathrm{i}}{e}^{\mathit{\omega N}}$

(1)

Here a is the crack length/depth; a_i is the initial crack size, which is often referred to as the equivalent initial flaw size (EIFS) or the equivalent precrack size (EPS) [9]; N is the number of cycles, or flight hours; and ω is a constant.

While the operators of military aircraft had long been aware of the problem of aging of an aircraft [3], public awareness of the problem first arose via the Aloha Airlines accident in April 1989 [10] which involved failure due to the presence of multisite damage in the fuselage lap joint of a Boeing 737-200 aircraft. Indeed, despite the fact that there were few casualties involved, it continues to be described as the event which first brought the aging aircraft issue to the attention of the general public and to those who have responsibility to ensure aircraft safety. The extent of the problems associated with fuselage lap joints in civil transport aircraft was further illustrated by the April 2011 incident whereby cracking in a fuselage lap joint in a Southwest Airlines Boeing 737-300 aircraft resulted in a large 1.52 m (5 ft) hole in the roof [11]. This incident led to the grounding of 79 of Southwest's older Boeing 737 aircraft [11] and to the cancellation of almost 700 flights. Subsequent inspections, which found cracks in a total of four Southwest aircraft [12], led to the US Federal Aviation Administration (FAA) mandating the inspection of 175 Boeing 737 aircraft that had seen more than 35,000 pressurisation cycles. The problem of cracking in fuselage lap joints was not confined to Boeing 737 aircraft. On 26 October 2010, an American Airlines 757-200 aircraft was forced to land at Miami International Airport due to a sudden decompression arising from cracking in a fuselage joint [13]. This aircraft had experienced less than 23,000 cycles. This led to the discovery of cracking in other 757 aircraft and a subsequent January 2011 FAA Airworthiness Directive [13] mandating the inspection of all 757-200 and 757-300 aircraft.

As a result of these incidents, and other considerations, the FAA introduced the concept of a limit of viability (LOV), defined as the onset of multisite and/or multielement damage, which the FAA now uses to define (or limit) the operational life of civil transport aircraft [13,14].

Thus given the central role that fatigue, fracture mechanics and damage tolerance play in aircraft design and sustainment, the first four chapters of this book focus on the following:

• The evolution of fatigue design requirements for aircraft structures with an emphasis on requirements, with design and operational issues also being addressed (Chapter Two).

• Typical fatigue initiating discontinuities in metallic aircraft structures and the lead crack concept. (Chapter Three).

• Practical computational fracture mechanics for use in assessing aircraft structural integrity (Chapter Four).

• Methods for computing/predicting the growth of cracks that arise from naturally occurring material discontinuities in operational aircraft (Chapter Five).

Chapters Two–Five are closely linked in that they each discuss the fact that the growth of ‘lead’ cracks [15], which are defined as the fastest growing cracks in the airframe and which (as a result) set both the inspection intervals and the operational life of the fleet, is generally exponential and as such follows Eq. (1). Chapter Two shows that, in the absence of severe corrosion, for aluminium alloy airframes the mean value of the EPS (EIFS) is ~ 0.01 mm.

Chapter Five shows that the exponent ω in the exponential growth law is approximately proportional to the cube of the stress [16]. Chapter Five explains that this cubic approximation is now used by the Royal Australian Air Force (RAAF) for the F/A-18 Classic Hornet, the AP3C (Orion) and the Pilatus Porter PC9 fleets [17–19]. It is further shown that crack growth in operational aircraft and in full-scale fatigue tests tested under an operational flight load spectra can be collapsed onto a single ‘master curve’ regardless of the material or the flight load spectrum.

Chapter Five also shows that, as shown in Ref. [8], the growth of both long and short cracks can be captured by the Hartman–Schijve variant of the NASGRO crack growth equation. In this context, it is shown that for cracks that arise and grow from small material discontinuities in operational aircraft the Hartman–Schijve equation can be approximated by a simple Paris crack growth equation with the exponent and the constant of proportionality determined from tests on ASTM E647-13a long crack specimens. The ability of the Hartman–Schijve crack growth equation to compute accurately the growth of cracks in 7075-T6 P3C Orion test specimen with intergranular cracking at a dome nut hole that has been repaired using supersonic particle deposition (SPD) is further highlighted in Chapter Sixteen. These findings are important since Chapters Twelve and Thirteen subsequently show that a variant of the Hartman–Schijve equation with Δ K replaced by Δ√ G, where G is the energy release rate, also captures the growth of disbonds in adhesively bonded joints and delamination growth in composites [20–23]. As such the Hartman–Schijve equation can be thought of as a unified formulation that can be used when assessing the original airframe and the damage tolerance of any subsequent structural repair.

In this context, it should be noted that before the Hartman–Schijve equation, or any other crack growth equation, can be used to predict/compute crack growth in an operational structure it is first necessary to determine the relationship between the stress intensity factor K and the crack length/depth. To this end, Chapter Four presents simple computational tools, both three-dimensional (3D) weight function and 3D finite element-based approaches, for determining the stress intensity factors associated with small sub-mm cracks in realistic complex geometries under arbitrary flight loads. Since, as explained in the fatigue test standard ASTM E647-13a, the majority of the fatigue life of an airframe is generally consumed in growing from a small sub-mm material discontinuity to a size that is readily detectable using modern nondestructive inspection techniques attention is focused on small initial cracks that first grow as a complex 3D shape and then transition into a through-the-thickness flaws with an oblique (part) elliptical crack front.

At this stage, it should be noted that Kinzie and Peeler [24] have shown how the problem of aging aircraft is particularly acute in the military sphere and how it has been compounded by US Congress, Public Law 107-314 Sec: 1067 which is entitled: “Prevention and mitigation of corrosion of military equipment and infrastructure.” One impact of this law is that the effect of corrosion on the structural integrity of USAF, US Army, US Navy aircraft and other Navy weapons platforms must be now quantified and managed as per cracking, that is, in a damage-tolerant manner. In this context, the June 2007 Report to Congress by the Under Secretary of the Department of Defense (Acquisition, Technology and Logistics) [25] estimated the cost of corrosion associated with ...

Table of contents

• Cover image
• Title page
• Table of Contents
• Copyright
• Contributors
• Chapter One: Rationale and Organisation
• Chapter Two: Fatigue Requirements for Aircraft Structures
• Chapter Three: Typical Fatigue-Nucleating Discontinuities in Metallic Aircraft Structures
• Chapter Four: Practical Computational Fracture Mechanics for Aircraft Structural Integrity
• Chapter Five: Crack Growth From Naturally Occurring Material Discontinuities
• Chapter Six: Adhesively Bonded Repair/Reinforcement of Metallic Airframe Components: Materials, Processes, Design and Proposed Through-Life Management
• Chapter Seven: Surface Treatment and Repair Bonding
• Chapter Eight: Analysis, Design and Assessment of Composite Repairs to Operational Aircraft
• Chapter Nine: Repair of Multisite Damage in Civil Transport Aircraft: An Example of the Damage-Tolerant Design of Composite Repairs
• Chapter Ten: The F111C Wing Pivot Fitting Repair and its Implications for the Design/Assessment of Bonded Joints and Composite Repairs
• Chapter Eleven: Development and Validation of Bonded Composite Doubler Repairs for Commercial Aircraft
• Chapter Twelve: Computing the Growth of Naturally-Occurring Disbonds in Adhesively-Bonded Joints
• Chapter Thirteen: Delamination Growth in Polymer-Matrix Fibre Composites and the Use of Fracture-Mechanics Data for Material Characterization and Life Prediction
• Chapter Fourteen: Introduction to Supersonic Particle Deposition
• Chapter Fifteen: Additive Metal Technologies for Aerospace Sustainment
• Chapter Sixteen: Applications of SPD to Enhance the Structural Integrity of Corroded Airframes
• Chapter Seventeen: Application of SPD to Enhance the Structural Integrity of Fuseage Skins and Centre Barells
• Chapter Eighteen: Multiplicative Manufacturing and Aircraft Sustainment
• Index