Auxetic Textiles

Hong Hu, Minglonghai Zhang, Yanping Liu

• Publisher: Woodhead Publishing
• Year: 2019
• Print ISBN: 9780081022115
• eBook ISBN: 9780081022122
• Topic: Technology & Engineering
• Subtopic: Materials Science
• Index: Technology & Engineering

Auxetic Textiles provides a detailed introduction to the basic properties of auxetic materials and how they differ from conventional materials, particularly auxetic textiles, such as polymers, fibers, yarns, fabrics and textile composites. The book discusses the beneficial properties of auxetic structures in textiles and how to translate those benefits into actual materials development. Sections cover the deformation mechanism of textile structures to achieve auxetic behavior and the modelling and simulation of auxetic textile structures. Finally, the book provides expert insights into potential application areas.Cutting across textiles disciplines, from technical textiles and advanced composites, to fashion and design, the book is a valuable introduction to the field for newcomers, with potent insights into the potential of these materials.- Introduces the concept of auxetic materials and their differences from conventional materials- Provides a practical guide to the mechanics of achieving auxetic properties in textile materials, including polymers, fibers, yarns, fabrics and composites- Reviews and links up research and development in auxetic materials with the textile industry, helping enable the development of a range of new applications

1

Introduction

Abstract

This chapter introduces the definition of Poisson’s ratio and briefly discusses its bounds from the point of view of classical elasticity theory. The enhancements of the mechanical and physical properties of materials due to auxetic or negative Poisson’s ratio behaviour are presented. The classifications of auxetic materials and auxetic textiles and a brief introduction on each class are also given.

Keywords

Poisson’s ratio; elasticity theory; mechanical properties; auxetic textiles

1.1 Definition of Poisson’s ratio

For ordinary materials in the world, it is a common sense that when materials are stretched or compressed in one direction, they contract or expand in the other direction perpendicular to the loading direction correspondently, as shown in Fig. 1.1A and B. For each type of material the contraction or expansion against the stretching or compression can be defined by a specific ratio known as Poisson’s ratio.

Figure 1.1 Schematic illustration for the deformation of materials with positive Poisson’s ratio: (A) under stretching; (B) under compression.

Therefore the Poisson’s ratio v is defined as the negative ratio between the strain in the transverse direction ${\epsilon }_T$

and the strain in the loading direction ${\epsilon }_L$

.

$\nu =-\frac{{\epsilon }_T}{{\epsilon }_L}$ (1.1)

(1.1)

The negative sign introduced in Eq. (1.1) is used to characterise the common and even intuitive phenomenon that stretching is expected to make materials thinner and compression results in bulge.

1.2 Nonconventional behaviour of auxetic materials

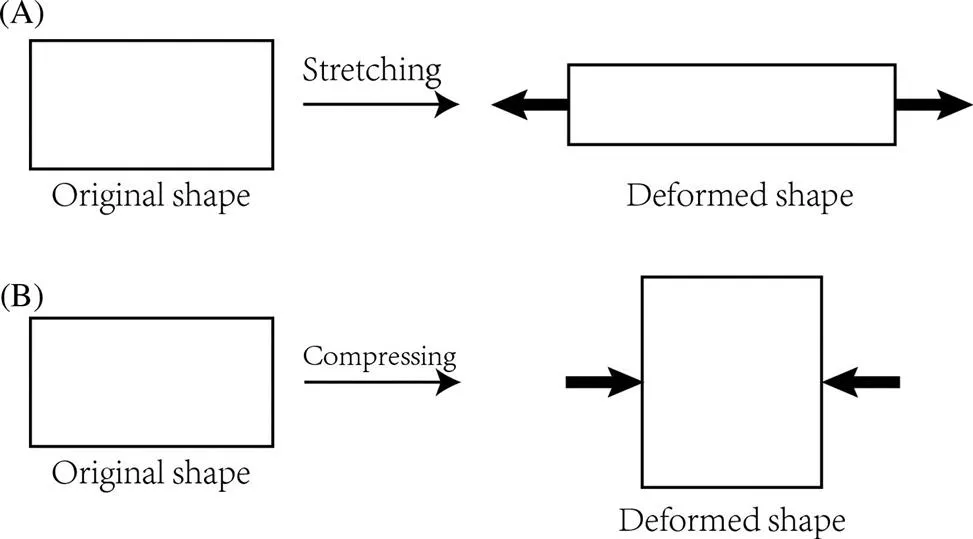
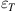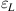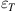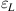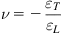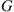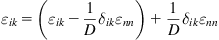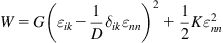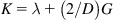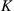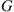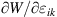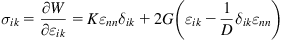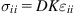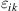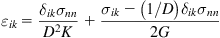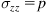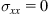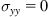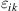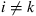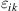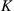1.2.1 Definition of auxetic materials

It is logical to think that Poisson’s ratio is positive, and for most of the materials in engineering, $\nu$

lies in the range from 0.2 to 0.5 [1]. Actually, the negative value of Poisson’s ratio does not contradict the classical elasticity, although it sounds incredible. Bounds for the Poisson’s ratio have been sufficiently discussed in literature. As early as 1848, Saint-Venant [2] suggested that the Poisson’s ratio may be negative in anisotropic materials and also may be greater than 0.5 for the first time in history. The limitation of the Poisson’s ratio (between −1 and 0.5) for isotropic materials was given by Fung [3] in 1965 according to the mathematical theory of elasticity. Similar conclusion was also reported elsewhere [4–6]. Based on the first law of thermodynamics, classical elasticity posits a free energy $W$

for isotropic body as a function of the strain tensor [4]:

$W=\frac{1}{2}\lambda {\epsilon }_{ii}^2+G{\epsilon }_{ik}^2$ (1.2)

(1.2)

where the general summation rule on repeated indices was used in the text book by Landau and Lifshitz [4], and the quantities $\lambda$

and $G$

are called Lamé coefficients ($G$

is also called the shear modulus).

Since any deformation of bodies can be represented as the sum of a pure shear and a hydrostatic compression, an identical expression for the strain tensor can be given as

${\epsilon }_{ik}=\left({\epsilon }_{ik}-\frac{1}{D}{\delta }_{ik}{\epsilon }_{nn}\right)+\frac{1}{D}{\delta }_{ik}{\epsilon }_{nn}$ (1.3)

(1.3)

where δ_ik is Kronecker delta and D = 2, 3 refers to the numbers of dimensions. What should be noted is that the values of subscripts i, k, n are x, y with D=2 while that are x, y, z with D=3. As mentioned by Landau and Lifshitz [4], the first term on the right is a pure shear, and the second term is a hydrostatic compression.

By using Eqs. (1.2) and (1.3) a general expression for the free energy of a deformed isotropic body in D dimension is given as follows [5]:

$W=G{\left({\epsilon }_{ik}-\frac{1}{D}{\delta }_{ik}{\epsilon }_{nn}\right)}^2+\frac{1}{2}K{\epsilon }_{nn}^2$ (1.4)

(1.4)

where $K=\lambda +\left(2/D\right)G$

and the quadratic Eq. (1.4) is positive definite if and only if the quantities $K$

and $G$

are positive, that is $K>0$

,$G>0$

.

The stress tensor can be obtained by calculate the derivatives $\partial W/\partial {\epsilon }_{ik}$

:

${\sigma }_{ik}=\frac{\partial W}{\partial {\epsilon }_{ik}}=K{\epsilon }_{nn}{\delta }_{ik}+2G\left({\epsilon }_{ik}-\frac{1}{D}{\delta }_{ik}{\epsilon }_{nn}\right)$ (1.5)

(1.5)

Intuitively, we can find from Eq. (1.5) that

${\sigma }_{ii}=DK{\epsilon }_{ii}$ (1.6)

(1.6)

Then, it is not difficult to give the converse formula that expresses strain tensor ${\epsilon }_{ik}$

in terms of stress tensor ${\sigma }_{ik}$

:

${\epsilon }_{ik}=\frac{{\delta }_{ik}{\sigma }_{nn}}{D^{2}K}+\frac{{\sigma }_{ik}-\left(1/D\right){\delta }_{ik}{\sigma }_{nn}}{2G}$ (1.7)

(1.7)

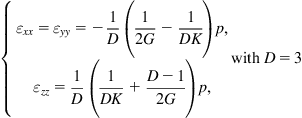
For a 3D isotropic body, just considering a hydrostatic pressure of $p$

along the z axis, we have ${\sigma }_{zz}=p$

, ${\sigma }_{xx}=0$

, ${\sigma }_{yy}=0$

, and all the component ${\sigma }_{ik}$

and ${\epsilon }_{ik}$

with $i\ne k$

are zero. The remaining components of ${\epsilon }_{ik}$

can be obtained according to Eq. (1.7):

$\{\begin{array}{c}{\epsilon }_{xx}={\epsilon }_{yy}=-\frac{1}{D}\left(\frac{1}{2G}-\frac{1}{DK}\right)p,\\ {\epsilon }_{zz}=\frac{1}{D}\left(\frac{1}{DK}+\frac{D-1}{2G}\right)p,\end{array}\mathrm{with}D=3$ (1.8)

(1.8)

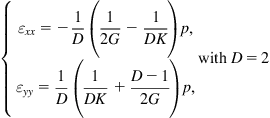
Similarly, in the case of the 2D isotropic body, considering a hydrostatic pressure of $p$

along the y axis, we can find

$\{\begin{array}{c}{\epsilon }_{xx}=-\frac{1}{D}\left(\frac{1}{2G}-\frac{1}{DK}\right)p,\\ {\epsilon }_{yy}=\frac{1}{D}\left(\frac{1}{DK}+\frac{D-1}{2G}\right)p,\end{array}\mathrm{with}D=2$ (1.9)

(1.9)

According to the definition of the Poisson’s ratio [see Eq. (1.1)], a general expression for the Poisson’s ratio of isotropic body in D dimensions can be given by using Eqs. (1.8) and (1.9):

$\nu =\frac{DK-2G}{\left(D-1\right)DK+2G}$ (1.10)

(1.10)

Since $K$

and $G$

...

Table of contents

• Cover image
• Title page
• Table of Contents
• Copyright
• Acknowledgements
• 1. Introduction
• 2. Auxetic structures and mechanisms
• 3. Auxetic polymers
• 4. Auxetic fibres and yarns
• 5. Auxetic fabrics based on knitted structures
• 6. Auxetic fabrics based on woven structures
• 7. Auxetic fabrics based on nonwoven structures
• 8. Auxetic fabrics based on braided structures
• 9. Auxetic fibre–reinforced composites
• 10. Applications of auxetic textiles
• Index