Application of Nuclear Magnetic Resonance Spectroscopy in Organic Chemistry

International Series in Organic Chemistry

L. M. Jackman, S. Sternhell, D. H. R. Barton, W. Doering

• Publisher: Pergamon
• Year: 2013
• Print ISBN: 9780080229539
• eBook ISBN: 9781483138596
• Edition: 2
• Topic: Physical Sciences
• Subtopic: Chemistry
• Index: Chemistry

Applications of Nuclear Magnetic Resonance Spectroscopy in Organic Chemistry, Second Edition focuses on the applications of nuclear magnetic resonance spectroscopy to problems in organic chemistry and the theories involved in this kind of spectroscopy. The book first discusses the theory of nuclear magnetic resonance, including dynamic and magnetic properties of atomic nuclei, nuclear resonance, and relaxation process. The manuscript also examines the experimental method. Topics include experimental factors that influence resolution and the shapes of absorption lines; measurement of line positions and identification of the chemical shift; and measurement of intensities. The text reviews the theories of chemical effects in nuclear magnetic resonance spectroscopy and spin-spin multiplicity and the theory and applications of multiple irradiation. The book also tackles the theory of chemical shift, including the classification of shielding effects, local diamagnetic proton shielding, solvent effects, and contact shifts. The publication is a dependable source of data for readers interested in the applications of nuclear magnetic resonance spectroscopy.

PART 1

An introduction to the theory and practice of nuclear magnetic resonance spectroscopy

Outline

Chapter 1: THEORY OF NUCLEAR MAGNETIC RESONANCE

Chapter 2: THE EXPERIMENTAL METHOD

CHAPTER 1-1

THEORY OF NUCLEAR MAGNETIC RESONANCE

Publisher Summary

Apart from the use of atomic numbers and isotopic weights, the organic chemist has largely developed his subject without any special knowledge of the properties of atomic nuclei. The recent advent of nuclear magnetic resonance spectroscopy and, to a much lesser extent, microwave and pure quadrupole spectroscopy has altered this state of affairs, and organic chemists of the present generation have now to become acquainted with certain subjects hitherto the domain of the nuclear physicist and the spectroscopist. In a uniform magnetic field, the angular momentum of a nucleus is quantized, the nucleus taking up one of (2I + 1) orientations with respect to the direction of the applied field. Each orientation corresponds to a characteristic potential energy of the nucleus equal to μ. H_o.cos θ where H_o is the strength of the applied field and the angle θ is the angle that the spin axis of the nucleus makes with the direction of the applied field. I and μ define the number and energies of the possible spin states that the nuclei of a given isotope can take up in a magnetic field of known strength. A transition of a nucleus from one spin state to an adjacent state may occur by the absorption or emission of an appropriate quantum of energy.

A DYNAMIC AND MAGNETIC PROPERTIES OF ATOMIC NUCLEI

Apart from the use of atomic numbers and isotopic weights, the organic chemist has largely developed his subject without any special knowledge of the properties of atomic nuclei. The recent advent of n.m.r. spectroscopy and, to a much lesser extent, microwave and pure quadrupole spectroscopy, has altered this state of affairs and organic chemists of the present generation have now to become acquainted with certain subjects hitherto the domain of the nuclear physicist and spectroscopist. Thus today a table of atomic weights of those elements commonly encountered by the organic chemist might usefully include other nuclear properties such as spin numbers, nuclear magnetic moments, and nuclear electric quadrupole moments.

Of these additional nuclear properties the spin number, I, and the nuclear magnetic moment, μ are of particular interest; the nuclear electric quadrupole moment, Q, will enter only occasionally into our discussions.

The nuclei of certain isotopes possess an intrinsic spin; that is they are associated with an angular momentum. The total angular momentum of a nucleus is given by (h/2π) · [I(I + 1)] in which h is Planck’s constant and I is the nuclear spin or spin number which may have the values 0,

, 1,

,… depending on the particular isotopic nucleus (I= 0 corresponds to a nucleus which does not possess a spin). Since atomic nuclei are also associated with an electric charge, the spin gives rise to a magnetic field such that we may consider a spinning nucleus as a minute bar magnet the axis of which is coincident with the axis of spin.^† The magnitude of this magnetic dipole is expressed as the nuclear magnetic moment, μ, which has a characteristic value for all isotopes for whichI is greater than zero.

In a uniform magnetic field the angular momentum of a nucleus (I > 0) is quantized, the nucleus taking up one of (2I + 1) orientations with respect to the direction of the applied field. Each orientation corresponds to a characteristic potential energy of the nucleus equal to μ· H₀· cos θ where H₀ is the strength of the applied field and the angleθ is the angle which the spin axis of the nucleus makes with the direction of the applied field. The importance of I and μ in our discussion is that they define the number and energies of the possible spin states which the nuclei of a given isotope can take up in a magnetic field of known strength. A transition of a nucleus from one spin state to an adjacent state may occur by the absorption or emission of an appropriate quantum of energy.

Nuclei of isotopes for which

are usually associated with an asymmetric charge distribution which constitutes an electric quadrupole. The magnitude of this quadrupole is expressed as the nuclear quadrupole moment Q.

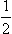
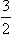
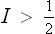
B NUCLEAR RESONANCE

Although the literature contains several detailed mathematical treatments of the theory of nuclear magnetic resonance which are based on microphysical²⁶⁵,¹⁹²⁹ or macrophysical²⁶³,²⁶⁴,¹⁹²⁹ concepts we will be content to develop the theory, as far as possible, in a purely descriptive manner by stating in words the results of the physicists’ equations. In doing so we will no doubt lose the elements of exactness but as organic chemists we will gain tangible concepts of considerable utility, which would otherwise be lost to all but those possessing the necessary mathematical background.

The starting point of our discussion is a consideration of a bare nucleus, such as a proton, in a magnetic field of strength H₀. Later we will consider collections of nuclei. We will also add the extranuclear electrons and ultimately we will build the atoms into molecules. We have just seen that certain nuclei possess two very important properties associated with spin angular momentum. These properties are the spin number I and the magnetic moment μ. We are only concerned with the nuclei of those isotopes for which these two quantities are not equal to zero.

When such a nucleus is placed in a static uniform magnetic field H₀ it takes up one of (2I +1) orientations which are characterized by energies dependent on the magnitudes of μ and H₀. If the bare nucleus is a proton, which has a spin number I equal to one half, we can liken it to a very tiny bar magnet. A large bar magnet is free to take up any possible orientation in the static field so that there are an infinite number of permissible energy states. Quantum mechanics tells us that the tiny proton magnet is restricted to just two possible orientations [(2I + 1) = 2], in the applied field and these can be considered to be a low energy or parallel orientation in which the magnet is aligned with the field and a high energy or anti-parallel orientation in which it is aligned against the field (i.e. with its N. pole nearest the N. pole of the static field). Since these two orientations correspond to two energy states it should be possible to induce transitions between them and the frequency, ν, of the electromagnetic radiation which will effect such transitions is given by the equation

(1-1-1)

where β_N is a constant called the nuclear magneton. Equation (1-1-1) may be rewritten as (1-1-2)

(1-1-2)

where γ is known as the gyromagnetic ratio. The absorption or emission of the quantum of energy hv causes the nuclear magnet to turn over or “flip” from one orientation to the other. For nuclei with spin numbers greater than

there will be more than two possible orientations (3 for I = 1, 4 for I=

, etc.) and in each case a set of equally spaced energy levels results. Again, electromagnetic radiation of appropriate frequency can cause transitions between the various levels with the proviso (i.e. selection rule) that only transitions between adjacent levels are allowed. Since the energy levels are equally spaced...

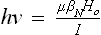
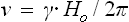
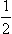
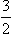
Table of contents

• Cover image
• Title page
• Table of Contents
• INTERNATIONAL SERIES IN ORGANIC CHEMISTRY
• Copyright
• Dedication
• PREFACE
• PREFACE TO THE 1st EDITION
• EDITORIAL PREFACE TO THE 2nd EDITION
• PART 1: An introduction to the theory and practice of nuclear magnetic resonance spectroscopy
• PART 2: Theory of chemical effects in nuclear magnetic resonance spectroscopy
• PART 3: Applications of the chemical shift
• PART 4: Spin-spin coupling
• PART 5: Applications of time-dependent phenomena
• REFERENCES
• INDEX