Leonhard Euler

Life, Work and Legacy

Robert E. Bradley, Ed Sandifer

• Publisher: Elsevier Science
• Year: 2007
• eBook ISBN: 9780080471297
• Topic: Mathematics
• Subtopic: Algebra
• Index: Mathematics

The year 2007 marks the 300th anniversary of the birth of one of the Enlightenment's most important mathematicians and scientists, Leonhard Euler. This volume is a collection of 24 essays by some of the world's best Eulerian scholars from seven different countries about Euler, his life and his work. Some of the essays are historical, including much previously unknown information about Euler's life, his activities in the St. Petersburg Academy, the influence of the Russian Princess Dashkova, and Euler's philosophy. Others describe his influence on the subsequent growth of European mathematics and physics in the 19th century. Still others give technical details of Euler's innovations in probability, number theory, geometry, analysis, astronomy, mechanics and other fields of mathematics and science.- Over 20 essays by some of the best historians of mathematics and science, including Ronald Calinger, Peter Hoffmann, Curtis Wilson, Kim Plofker, Victor Katz, Ruediger Thiele, David Richeson, Robin Wilson, Ivor Grattan-Guinness and Karin Reich- New details of Euler's life in two essays, one by Ronald Calinger and one he co-authored with Elena Polyakhova- New information on Euler's work in differential geometry, series, mechanics, and other important topics including his influence in the early 19th century

Cyclotomy: From Euler through Vandermonde to Gauss

Olaf Neumann Mathematisches Institut, Friedrich-Schiller-Universität Jena, D-07737 Jena Germany

The word “cyclotomy” is of Greek origin and means “division of the circle.” As a mathematical term it denotes the subdivision of a full circle line into a given number of equal parts. Consider the unit circle x² + y² = 1 in the Euclidean plane with Cartesian coordinates (x, y). If this circle is divided into n equal parts beginning with the point (1, 0) then the other division points will have coordinates $\left(cos\frac{2\mathit{\pi }\cdot \mathit{k}}{\mathit{n}},sin\frac{2\mathit{\pi }\cdot \mathit{k}}{\mathit{n}}\right)$

where k runs from 1 to (n − 1). All those points form the edges of a regular n-sided polygon. It is well-known that by means of the imaginary quantity $\mathit{i}:=\sqrt{-1}$

one can prove the formula

${\left(cos\mathit{\alpha }+\mathit{i}\cdot sin\mathit{\alpha }\right)}^{\mathit{n}}=cos\mathit{n\alpha }+\mathit{i}\cdot sin\mathit{n\alpha }$

(1)

which is usually called de Moivre’s formula. But in the form (1) it is due to Leonhard Euler (1707–1783), see [Euler 1748], cap. VIII. In particular, the n arguments $\mathit{\alpha }=\frac{2\mathit{\pi }\cdot \mathit{k}}{\mathit{n}}$

with 0 ≤ k ≤ n − 1 provide us with the n powers 1, ζ_n, ζ_n², …, ζ_n^{n − 1} of the complex number ${\mathit{\zeta }}_{\mathit{n}}:=cos\frac{2\mathit{\pi }}{\mathit{n}}+\mathit{i}\cdot sin\frac{2\mathit{\pi }}{\mathit{n}}$

:

${\zeta }_n^k=cos\frac{2\mathit{\pi }\cdot \mathit{k}}{\mathit{n}}+\mathit{i}\cdot sin\frac{2\mathit{\pi }\cdot \mathit{k}}{\mathit{n}}\left(0\le \mathit{k}\le \mathit{n}-1\right)$

(2)

satisfying the equation

${\mathit{x}}^{\mathit{n}}-1=0.$

(3)

This means that Eqn. (3) has exactly n roots which are given in the transcendental form (2) and which are the powers of one of them, namely ζ_n. For these powers we shall adopt the name nth roots of unity common today among mathematicians. If the exponent i is prime to n then ζ_n^i...

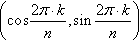
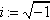
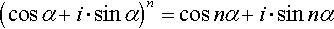
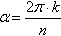
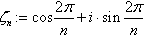
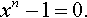
Table of contents

• Cover image
• Title page
• Table of Contents
• Copyright page
• Foreword
• Introduction
• Leonhard Euler: Life and Thought
• Leonhard Euler and Russia
• Princess Dashkova, Euler, and the Russian Academy of Sciences
• Leonhard Euler and Philosophy
• Images of Euler
• Euler and Applications of Analytical Mathematics to Astronomy
• Euler and Indian Astronomy
• Euler and Kinematics
• Euler on Rigid Bodies
• Euler’s Analysis Textbooks
• Euler and the Calculus of Variations
• Euler, D’Alembert and the Logarithm Function
• Some Facets of Euler’s Work on Series
• The Geometry of Leonhard Euler
• Cyclotomy: From Euler through Vandermonde to Gauss
• Euler and Number Theory: A Study in Mathematical Invention
• Euler and Lotteries
• Euler’s Science of Combinations
• The Truth about Königsberg
• The Polyhedral Formula
• On the Recognition of Euler among the French, 1790-1830
• Euler’s Influence on the Birth of Vector Mechanics
• Euler’s Contribution to Differential Geometry and its Reception
• Euler’s Mechanics as a Foundation of Quantum Mechanics
• Index