The Language of Shape

The Role of Curvature in Condensed Matter: Physics, Chemistry and Biology

S. Hyde, Z. Blum, T. Landh, S. Lidin, B.W. Ninham, S. Andersson, K. Larsson

• Publisher: Elsevier Science
• Year: 1996
• Print ISBN: 9780444815385
• eBook ISBN: 9780080542546
• Topic: Physical Sciences
• Subtopic: Differential Geometry

This book develops the thesis that structure and function in a variety of condensed systems - from the atomic assemblies in inorganic frameworks and organic molecules, through molecular self-assemblies to proteins - can be unified when curvature and surface geometry are taken together with molecular shape and forces. An astonishing variety of synthetic and biological assemblies can be accurately modelled and understood in terms of hyperbolic surfaces, whose richness and beauty are only now being revealed by applied mathematicians, physicists, chemists and crystallographers. These surfaces, often close to periodic minimal surfaces, weave and twist through space, carving out interconnected labyrinths whose range of topologies and symmetries challenge the imaginative powers.The book offers an overview of these structures and structural transformations, convincingly demonstrating their ubiquity in covalent frameworks from zeolites used for cracking oil and pollution control to enzymes and structural proteins, thermotropic and lyotropic bicontinuous mesophases formed by surfactants, detergents and lipids, synthetic block copolymer and protein networks, as well as biological cell assemblies, from muscles to membranes in prokaryotic and eukaryotic cells. The relation between structure and function is analysed in terms of the previously neglected hidden variables of curvature and topology. Thus, the catalytic activity of zeolites and enzymes, the superior material properties of interpenetrating networks in microstructured polymer composites, the transport requirements in cells, the transmission of nerve signals and the folding of DNA can be more easily understood in the light of this.The text is liberally sprinkled with figures and colour plates, making it accessible to both the beginning graduate student and researchers in condensed matter physics and chemistry, mineralogists, crystallographers and biologists.

Chapter 1

The Mathematics of Curvature

1.1 Introductory remarks

This book deals with shape and form, and especially the role of curvature in the natural sciences. Our search is for a connection between structure and function posed by D’Arcy Thompson in his famous book “On Growth and Form” [1] almost a century ago. Our theme will be that curvature, a neglected dimension, is central. Some of the curved surfaces that will preoccupy us and recur are shown in the Appendix to this Chapter. The reader is invited to pursue them at once. They are not just computer generated art or mathematical abstractions, and will be seen later to be ubiquitous in nature. They represent situations as diverse as:

• equipotential surfaces dividing space between the atoms of a crystal

• real structures formed spontaneously by the constituent molecules of biological membranes

• the shapes of bio-macromolecules, from proteins to starch

Euclidean geometry underlies practically all of science and our intuition has depended on it. The shapes provided: planes, cylinders, spheres, polyhedra, all have constant or even zero curvature. Only in theoretical physics, in subjects like general relativity where the curvature of space-time is essential, has non-Euclidean geometry and especially so-called hyperbolic geometry played any part in the scheme of things. The scientific community has been prepared to leave such matters to physicists alone. It can do so no longer, and the idea of curvature is becoming an essential tool to the understanding of many phenomena.

This Chapter is concerned with some of the mathematical tools required to describe special properties of curved surfaces. The tools are to be found in differential geometry, analytical function theory, and topology. General references can be found at the end of the Chapter. The reader uninterested in the mathematics can skip the equations and their development. The ideas we want to focus on will be clear enough in the text. A particular class of saddle-shaped (hyperbolic) surfaces called minimal surfaces will be treated with special attention since they are relatively straightforward to treat mathematically and do form good approximate representations of actual physical and chemical structures.

1.2 Curvature

The concept of curvature was developed by Isaac Newton in the middle of the 17^th century, as a natural extension to his work on the calculus. At that time, the determination of the perimeter of planar curves and the area under curves were major problems. In particular, Newton’s new analytical tools allowed him to determine the “quadrature” (area) of a circle. It occurred to Newton that the radius of the circle of best fit to an arbitrary planar curve at all points on the curve was a useful measure, for which he coined the term “crookedness”[2]. This is curvature (Fig. 1.1).

Figure 1.1 The curvature of a planar curve at a point (P) is equal to the reciprocal of the radius of the circle of best fit to the curve at P, r.

The curvature of a planar curve relates arc length along the curve to changes of tangent vector (Fig. 1.2).

Figure 1.2 Tangents TP and QT at two points, P and Q, on a planar curve.

The tangents TP and QT in Fig. 1.2 subtend angles ψ, ψ+δψ with the x-axis, so that δψ is the angle between the two tangents. If δs is the length of the arc PQ along the curve, then

is the average curvature of the planar curve along the arc PQ. The curvature at the point P is defined to be the limit of this expression as Q approaches P, i.e.

If PQ is the arc of a circle of radius r, the angle δψ between the tangents at P and Q is equal to the angle subtended at the centre of the circle by the arc PQ, so that δs=rδψ, whence

. The curvature is constant at all points of a circle, and the radius is equal to the reciprocal of the curvature (Fig. 1.1). If the curve is described in cartesian coordinates by a function y=y(x):

so that:

The curvature, κ, is thus given by the expression:

(1.1)

If the positive value of the root of the denominator is taken, the sign of the curvature will be the same as that of

; i.e. positive if the curve lies above the tangent, and negative below it. At a point of inflection (or a straight line),

is zero and therefore the curvature is zero in these cases. The sign of the curvature signifies the convex or concave nature of the curve. It is also related to the side of the curve at which the centre of the circle of best fit is located (cf. Fig. 1.3).

Figure 1.3 The radii of curvature, r_P and r_Q at two points, P and Q, on a planar curve. The centres of the circles of best fit to the curve at P and Q lie on opposite sides of the curve and the curvature changes sign at the point of inflection on the curve between these points. The curvature at Q is positive and at P it is negative.

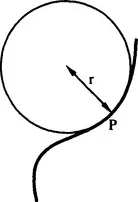
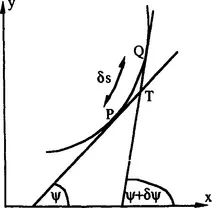
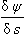
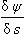
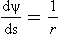
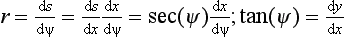
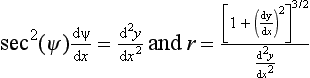
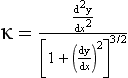
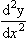
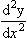
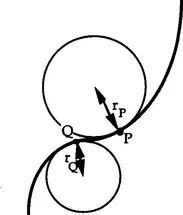
1.3 The differential geometry of surfaces

The curvatures of a surface are more complex entities, but can be understood as a generalisation of the curvature of planar curves. Imagine a plane containing a point P on the (smooth) surface, which contains the vector (n) passing through P, normal to the surface (Fig. 1.4).

Figure 1.4 The intersection of a surface with the plane...

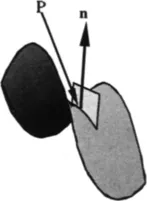
Table of contents

• Cover image
• Title page
• Table of Contents
• Copyright
• Acknowledgments
• Preface
• Chapter 1: The Mathematics of Curvature
• Chapter 2: The Lessons of Chemistry
• Chapter 3: Molecular Forces and Self-Assembly
• Chapter 4: Beyond Flatland: The Geometric Forms due to Self-Assembly
• Chapter 5: Lipid Self-Assembly and Function In Biological Systems
• Chapter 6: Folding and Function In Proteins and DNA
• Chapter 7: Cytomembranes and Cubic Membrane Systems Revisited
• Chapter 8: Some Miscellaneous Speculations
• Index (All names are capitalised.)