Kinetics of Aggregation and Gelation

F. Family, D.P. Landau

• Publisher: North Holland
• Year: 2012
• Print ISBN: 9780444869128
• eBook ISBN: 9780444596581
• Topic: Physical Sciences
• Subtopic: Physical & Theoretical Chemistry

Kinetics of Aggregation and Gelation presents the proceedings of the International Topical Conference on Kinetics of Aggregation and Gelation held on April 2-4, 1984 in Athens, Georgia. The purpose of the conference was to bring together international experts from a wide variety of backgrounds who are studying phenomena inherently similar to the formation of large clusters by the union of many separate, small elements, to present and exchange ideas on new theories and results of experimental and computer simulations. This book is divided into 57 chapters, each of which represents an oral presentation that is part of a unified whole. The book begins with a presentation on fractal concepts in aggregation and gelation, followed by presentations on topics such as aggregative fractals called ""squigs""; multi-particle fractal aggregation; theory of fractal growth processes; self-similar structures; and interface dynamics. Other chapters cover addition polymerization and related models; the kinetic gelation model; a new model of linear polymers; red cell aggregation kinetics; the Potts Model; aggregation of colloidal silica; the ballistic model of aggregation; stochastic dynamics simulation of particle aggregation; particle-cluster aggregation; kinetic clustering of clusters; computer simulations of domain growth; and perspectives in the kinetics of aggregation and gelation. This book will be of interest to practitioners in the fields of chemistry, theoretical physics, and materials engineering.

FRACTAL CONCEPTS IN AGGREGATION AND GELATION: AN INTRODUCTION

H. Eugene STANLEY, Center for Polymer Studies and Department of Physics, Boston University, Boston MA 02215 USA

This review talk is a follow-up to review talks delivered by the author at the December 1982 Santa Barbara meeting and the August 1983 Exxon meeting. At that time, many workers in this field characterized a class of aggregates by a single parameter–the fractal dimension d_f–which is the slope of a log-log plot of cluster mass vs. length scale (cluster radius). Now at least nine separate cluster parameters are found to be linear when plotted against cluster radius on log-log paper. Accordingly, there are at least nine different fractal dimensions in use at the present time. The situation is reminiscent of critical phenomena just before Widom and Kadanoff introduced scaling relations: there were then a vast number of seemingly independent critical exponents. Accordingly, we also review some of the newly-emerging relationships between these fractal dimensions.

The work in this talk was done in collaboration with A. Coniglio, Z. Djordjevic, S. Havlin, H.J. Herrmann, D.C. Hong, N. Jan, F. Leyvraz, I. Majid, A. Margolina, and P. Meakin. It is also a pleasure to acknowledge at the outset interactions with A. Aharony, S. Alexander, Y. Gefen, P.G. de Gennes, I. Procaccia, D. Stauffer, and T. Witten. This talk is dedicated to those scientists who are still waiting for the opportunity to leave their country–were it not for this inalienable freedom, none of us would be here today.

It is not easy to give an elementary opening talk to a meeting populated by many experts! Hence I′ve chosen the main point to be that answers to an increasing number of physics questions can be expressed in terms of geometrical parameters called “fractal dimensions.” Presently there are as many notations for fractal dimensions as there are workers in the field. The notation we shall use has one advantage: there are no tidies, bars, or double bars to confuse the myopic reader. Instead, we shall use a subscript to denote “which” fractal dimensions is intended; although this notation may appear somewhat cumbersome at first, it has the virtue that one never doubts what quantity is under consideration.

1 FRACTAL DIMENSION OF ENTIRE CLUSTER AND THE FIELD SCALING POWER

The first fractal dimension we introduced into statistical mechanics is sometimes called “the” fractal dimension. It is d_f, the fractal dimension characterizing the dependence of the total mass on the characteristic length scale on which the fractal is examined. Thus we write

(1a)

In the 1977 paper that introduced fractals into percolation, it was noted that one reason for the possible interest in d_f is that it is equal to the magnetic scaling power y_h,

(1b)

Thus fractals provide a geometrical interpretation of what was previously an abstract mathematical quantity!

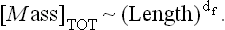
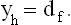
2 FRACTAL DIMENSION OF RED BONDS AND THE THERMAL SCALING POWER (“LINKS”)

Is there an analogous geometrical interpretation of the thermal scaling power y_T in percolation? A second fractal quantity was introduced in the 1977 paper in connection with the observation that the incipient infinite cluster in percolation consists of multiply-connected “blobs” joined by singly-connected “links.” Pike has made a computer simulation of this links/blobs decomposition, published in color in Physics Today, May 1983–the links are in red and blobs in blue, with the dangling ends in yellow. One defines d_red through

(2a)

with similar definitions for the blue and yellow. Coniglio in 1982 proved rigorously that

(2b)

Thus both scaling powers in percolation are directly related to geometrical parameters.

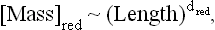
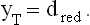
3 FRACTAL DIMENSION OF THE BACKBONE

Although there are only 2 scaling powers in percolation, there are many more fractal dimensions in use. In the remainder of this talk, we shall describe some of these. The reader may have a feeling of deja vu, since before Widom and Kadanoff made the scaling conjecture in 1965-1966, there were a vast constellation of critical exponents in use. It is possible that the large number of fractal dimensions that we now have will be reduced as relations are found among them.

Having mentioned the 1977 decomposition of the backbone of the incipient infinite cluster into blue blobs and red links, it is natural to consider the fractal dimension of the backbone itself. Thus we define

(3)

Why do we care about the backbone? Suppose we attach the terminals of a battery to two points of a percolation cluster. Then it is the backbone bonds that will carry current, and not the dangling ends. Thus we expect that the backbone will be related to the behavior of the electrical resistance.

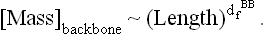
4 FRACTAL DIMENSION OF A RANDOM WALK

To see the relation directly, we must utilize the Einstein relation: the electrical conductivity is proportio...

Table of contents

• Cover image
• Title page
• Table of Contents
• Copyright
• PREFACE
• PROGRAM
• LIST OF PARTICIPANTS
• Chapter 1: FRACTAL CONCEPTS IN AGGREGATION AND GELATION: AN INTRODUCTION
• Chapter 2: ON THE AGGREGATIVE FRACTALS CALLED “SQUIGS”, WHICH INCLUDE RECURSIVE MODELS OF POLYMERS AND OF PERCOLATION CLUSTERS
• Chapter 3: ON 2D PERCOLATION CLUSTERS AND ON MULTI-PARTICLE FRACTAL AGGREGATION
• Chapter 4: THEORY OF FRACTAL GROWTH PROCESSES
• Chapter 5: SELF–SIMILAR STRUCTURES AND THE KINETICS OF AGGREGATION OF GOLD COLLOIDS
• Chapter 6: ELECTROSTATIC AGGREGATION AND INTERFACE DYNAMICS
• Chapter 7: PROPERTIES OF THE GROWING INTERFACE IN DIFFUSION-LIMITED AGGREGATION AND IN THE EDEN PROCESS
• Chapter 8: ADDITION POLYMERIZATION AND RELATED MODELS
• Chapter 9: OSCILLATIONS AND SCALING IN A KINETIC GELATION MODEL
• Chapter 10: KINETIC GELATION WITH A CONSTANT INITIATOR CREATION RATE
• Chapter 11: THE KINETIC GROWTH WALK: A NEW MODEL FOR LINEAR POLYMERS
• Chapter 12: MEASURING RED CELL AGGREGATION KINETICS WITH NUCLEAR MAGNETIC RESONANCE
• Chapter 13: MONTE CARLO SIMULATION OF VULCANIZATION
• Chapter 14: CLUSTER NUMBERS FROM THE POTTS MODEL
• Chapter 15: THE ATOM PROBE – A DIRECT TECHNIQUE FOR KINETIC MEASUREMENTS
• Chapter 16: A SMALL-ANGLE NEUTRON SCATTERING STUDY OF THE DECOMPOSITION OF Fe-28Cr-10.5Co
• Chapter 17: AGGREGATION OF COLLOIDAL SILICA
• Chapter 18: MEAN FIELD THEORY FOR A BALLISTIC MODEL OF AGGREGATION
• Chapter 19: LARGE-CELL MONTE CARLO RENORMALIZATION OF IRREVERSIBLE GROWTH PROCESSES
• Chapter 20: STOCHASTIC DYNAMICS SIMULATION OF PARTICLE AGGREGATION
• Chapter 21: OBSERVATION OF POWER-LAW CORRELATIONS IN SILICA-PARTICLE AGGREGATES BY SMALL-ANGLE NEUTRON SCATTERING
• Chapter 22: PARTICLE-CLUSTER AGGREGATION WITH FRACTAL PARTICLE TRAJECTORIES AND ON FRACTAL SUBSTRATES
• Chapter 23: SCALING PROPERTIES OF GROWTH BY KINETIC CLUSTERING OF CLUSTERS
• Chapter 24: CRITICAL DYNAMICS IN CLUSTER-CLUSTER AGGREGATION
• Chapter 25: THE STRUCTURE AND FRACTAL DIMENSION OF CLUSTER-CLUSTER AGGREGATES
• Chapter 26: COMPUTER SIMULATIONS OF DOMAIN GROWTH
• Chapter 27: RANDOM-FIELD ISING MODEL: DOMAIN GROWTH THEORY
• Chapter 28: RANDOM FIELD ISING MODEL: COMPUTER SIMULATIONS OF DOMAIN GROWTH
• Chapter 29: THE ELASTICITY AND VIBRATIONAL MODES OF PERCOLATING NETWORKS AND OTHER FRACTAL STRUCTURES
• Chapter 30: KINETICS OF RED BLOOD CELL AGGREGATION: AN EXAMPLE OF GEOMETRIC POLYMERIZATION
• Chapter 31: INTRINSIC PROPERTIES OF PERCOLATION CLUSTERS AND BRANCHED POLYMERS
• Chapter 32: BIASED DIFFUSION ON RANDOMLY GROWN PERCOLATING CLUSTERS
• Chapter 33: NONLINEAR RESPONSE AND METASTABILITY OF COULOMB SYSTEMS NEAR THE PERCOLATION THRESHOLD
• Chapter 34: THE STRUCTURE AND FRACTAL DIMENSION OF GENERALIZED DIFFUSION-LIMITED AGGREGATES
• Chapter 35: FREQUENCY SPECTRUM OF AN ELASTIC SIERPINSKI GASKET
• Chapter 36: PARTICLE DEPOSITION ON A FILTER MEDIUM
• Chapter 37: GROWTH OF CLUSTERS DURING IMBIBITION IN A NETWORK OF CAPILLARIES
• Chapter 38: EXPERIMENTAL MEASUREMENTS OF THE KINETIC EVOLUTION OF CLUSTER SIZE DISTRIBUTIONS WITH APPLICATIONS TO THE FRACTAL STRUCTURE OF ANTIGEN-ANTIBODY CLUSTERS
• Chapter 39: EXPERIMENTAL ANALYSIS OF DIFFUSION CONTROLLED COAGULATION USING AN OPTICAL PULSE PARTICLE SIZE ANALYZER
• Chapter 40: AGGREGATION KINETICS VIA SMOLUCHOWSKI’S EQUATION
• Chapter 41: CRITICAL EXPONENTS IN THE SMOLUCHOWSKI EQUATIONS OF COAGULATION
• Chapter 42: KINETICS OF REVERSIBLE CLUSTERING AND BRANCHING
• Chapter 43: KINETICS OF PHASE SEPARATION IN MIXTURES OF LINEAR AND BRANCHED POLYMERS
• Chapter 44: INHOMOGENEITY IN GELATION
• Chapter 45: RELATIONSHIP BETWEEN THE KINETIC AND STATISTICAL APPROACHES TO f-FUNCTIONAL POLYCONDENSATION
• Chapter 46: SMOLUCHOWSKI’s EQUATION WITH SURFACE INTERACTION AND EXPONENTS IN THE CLUSTER SIZE DISTRIBUTION
• Chapter 47: LIGHT SCATTERING STUDIES OF NUCLEATION OF POLYPROPYLENE
• Chapter 48: GLASSY RIGIDIFICATION PHENOMENA: IS THERE A UNIFIED PICTURE EMERGING?
• Chapter 49: DIFFUSION AND CONDUCTIVITY EXPONENTS NOT BASED ON THE ALEXANDER-ORBACH CONJECTURE
• Chapter 50: IRREVERSIBLE SELF AVOIDING WALKS
• Chapter 51: FRACTAL GEOMETRIES IN DECAY MODELS
• Chapter 52: DRIFT AND DIFFUSION IN A HOPPING MODEL WITH STRONG DISORDER
• Chapter 53: CORRECTIONS TO SCALING IN CLUSTER STATISTICS PROBLEMS—AN OVERVIEW OF RECENT RESULTS
• Chapter 54: CLUSTER STATISTICS AND SCALING IN A REGULAR MODEL OF DIFFUSION-CONTROLLED DEPOSITION
• Chapter 55: EXACT RNG FOR DISORDERED DIFFUSIVE SYSTEMS AND FLUIDS
• Chapter 56: FIBRIN AGGREGATES: FRACTAL OBJECTS WITH D = 1
• Chapter 57: PERSPECTIVES IN THE KINETICS OF AGGREGATION AND GELATION
• AUTHOR INDEX
• SUBJECT INDEX