Cell Physiology Source Book

Essentials of Membrane Biophysics

Nicholas Sperelakis

• Publisher: Academic Press
• Year: 2011
• eBook ISBN: 9780123877574
• Edition: 4
• Topic: Biological Sciences
• Subtopic: Biochemistry
• Index: Biological Sciences

Cell Physiology Source Book gathers together a broad range of ideas and topics that define the field. It provides clear, concise, and comprehensive coverage of all aspects of cellular physiology from fundamental concepts to more advanced topics. The 4e contains substantial new material. Most chapters have been thoroughly reworked. The book includes chapters on important topics such as sensory transduction, the physiology of protozoa and bacteria, and synaptic transmission.- Authored by leading researchers in the field- Clear, concise, and comprehensive coverage of all aspects of cellular physiology, from fundamental concepts to more advanced topics- Full color illustrations

Section II

Membrane Potential, Transport Physiology, Pumps, and Exchangers

Chapter 8 Diffusion and Permeability

Chapter 9 Origin of Resting Membrane Potentials

Chapter 10 Gibbs–Donnan Equilibrium Potentials

Chapter 11 Mechanisms of Carrier-Mediated Transport

Chapter 12 Active Ion Transport by ATP-Driven Ion Pumps

Chapter 13 Ca²⁺-ATPases

Chapter 14 Na⁺-Ca²⁺ Exchange Currents

Chapter 15 Intracellular Chloride Regulation

Chapter 16 Osmosis and Regulation of Cell Volume

Chapter 17 Intracellular pH Regulation

Chapter 8

Diffusion and Permeability

Nicholas Sperelakis and Jeffrey C. Freedman

Chapter Outline

I. Summary

II. Introduction

III. Fick’s Law of Diffusion

IV. Diffusion Coefficient

V. Diffusion Across a Membrane with Partitioning

VI. Permeability Coefficient

VII. Electrodiffusion

VIII. Special Transport Processes

IX. Ussing Flux Ratio Equation

Bibliography

I Summary

This chapter describes diffusion of uncharged particles and charged ions across membranes with and without partitioning and provides the relevant equations that govern such diffusion. The relationship between the diffusion coefficient (D) and the permeability coefficient (P) is presented, as well as the factors that determine these coefficients. The dependence of P on the mobility of an ion through the membrane under a voltage gradient is also described. Electrochemical potential is defined and the interconversion between flux and current is presented. Finally, the Ussing flux ratio equation is presented and examples of its significance are given. Relating to this, the concept of potential energy wells and barriers is presented, describing the movement of an ion through an ion channel.

II Introduction

In order to understand the fundamentals of membrane transport, as well as the mechanisms for development of the electrical resting potential (RP) of cells, it is first necessary to consider the basic processes of diffusion and membrane permeability. Therefore, this chapter discusses fundamental principles that are utilized in subsequent chapters in this book.

Molecules of gases and liquids and dissolved solutes are continuously in motion. The velocities of individual molecules vary tremendously, as do their kinetic energies (in accordance with the Maxwell–Boltzmann distribution). Diffusion is the process whereby particles in a gas or liquid tend to intermingle due to their spontaneous motion caused by thermal agitation. Any diffusing substance tends to move from regions of higher concentration to regions of lower concentration, until the substance is uniformly distributed at equilibrium. The molecules continue to move at equilibrium, but the net movement is zero. In the absence of convection, which refers to bulk flow of solvent, such as that caused by stirring, the movement of the molecules is by diffusion only. Diffusion occurs because of the random thermal motions of the molecules. Particles flow from a region of high concentration to one of low concentration. If a solution of high solute concentration is adjacent to one of low concentration, but separated by an imaginary plane, it is probable that more molecules per unit of time will be crossing the plane from the side of higher concentration to the side of lower concentration than in the opposite direction. There are fluxes (movements of molecules) in both directions (the unidirectional fluxes), but the net flux is from the side of higher concentration to the side of lower concentration.

Now, if the imaginary plane were replaced with a thin membrane permeable to the molecules, then the same situation would apply; the particles would diffuse from the side of higher concentration to the side of lower concentration across the membrane. In a living cell, it is usually assumed that the bulk solutions are relatively well mixed and diffusion of most substances through the cell membrane is much slower than that through a free solution. Therefore, diffusion through the membrane is the rate-limiting step. For simplicity, we assume that the solutions on either side are well stirred (although there may actually be unstirred layers near the membrane). We confine ourselves here to the diffusion of small molecules or ions across the cell membrane.

For thin membranes, we first consider the case of diffusion without partitioning, as illustrated in Fig. 8.1 (left), in which the diffusing molecule can freely enter the membrane. We will then introduce the effect of partitioning into the membrane, a process that involves a change of chemical potential upon entrance into the membrane phase, as illustrated in Fig. 8.1 (right). We disregard possible structural obstacles that may be a series of potential energy barriers within the membrane (Danielli, 1943).

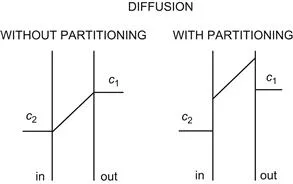
FIGURE 8.1 Concentration gradients across the membrane during diffusion without partitioning (left) and with partitioning (right).

III Fick’s Law of Diffusion

The fundamental law describing diffusion was enunciated by Adolph E. Fick in 1855, who noted a similarity between diffusion of solutes and Fourier’s law describing the flow of heat in solids. Fick’s law of diffusion was deduced theoretically in 1860 by James C. Maxwell from the kinetic theory of gases. The derivation of Fick’s law includes the following assumptions: (1) statistical laws apply; (2) the average duration of a collision is short compared to the average time between collisions, a condition pertaining to dilute solutions; (3) the particles move independently; (4) classical mechanics can be used to describe molecular collisions; (5) energy, momentum and mass are conserved in every collision; and (6) the diffusing solute particles are much larger than the solvent molecules of the liquid.

IV Diffusion Coefficient

Consider two compartments, separated by a membrane of thickness Δx, in which a substance diffuses from inside a cell (denoted as compartment i with high concentration c_i) across the cell membrane into the outside medium (denoted as compartment o with low concentration c_o). It is assumed that the temperature and pressure are the same in both compartments. For such a system, Fick’s first law of diffusion states that the flux density ( J, mol/s-cm²) is directly proportional to the concentration gradient dc/dx (mol/cm³/cm) across the membrane.

(8.1)

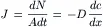
where dN/Adt (mol/(cm²·s) is the number (dN) of moles that diffuse across a unit area (A, cm²) of the membrane during an interval of time (dt, s). The diffusion coefficient D (cm²/s).indicates how much flux will occur for a given concentration gradient.

The concentration gradient in the steady state is equal to the difference in the concentration (Δc = c_o−c_i) of the solute o...

Table of contents

• Cover Image
• Table of Contents
• Title
• Copyright
• Dedication
• In Memoriam
• Contributors
• Foreword to the First Edition
• Foreword to the Second Edition
• Foreword to the Third Edition
• Foreword to the Fourth Edition
• Preface
• Section I Biophysical Chemistry, Metabolism, Second Messengers, and Ultrastructure
• Section II Membrane Potential, Transport Physiology, Pumps, and Exchangers
• Section III Membrane Excitability and Ion Channels
• Section IV Ion Channels as Targets for Toxins, Drugs, and Genetic Diseases
• Section V Synaptic Transmission and Sensory Transduction
• Section VI Muscle and Other Contractile Systems
• Section VII Protozoa and Bacteria
• Section VIII Specialized Processes: Photosynthesis and Bioluminescence
• Appendix: Excitability of Smooth Muscles: Some Basic Facts
• Index