Algorithmic Graph Theory and Perfect Graphs

Martin Charles Golumbic

• Publisher: North Holland
• Year: 2004
• Print ISBN: 9780444515308
• eBook ISBN: 9780080526966
• Edition: 2
• Topic: Mathematics
• Subtopic: Discrete Mathematics
• Index: Mathematics

Algorithmic Graph Theory and Perfect Graphs, first published in 1980, has become the classic introduction to the field. This new Annals edition continues to convey the message that intersection graph models are a necessary and important tool for solving real-world problems. It remains a stepping stone from which the reader may embark on one of many fascinating research trails.The past twenty years have been an amazingly fruitful period of research in algorithmic graph theory and structured families of graphs. Especially important have been the theory and applications of new intersection graph models such as generalizations of permutation graphs and interval graphs. These have lead to new families of perfect graphs and many algorithmic results. These are surveyed in the new Epilogue chapter in this second edition.- New edition of the "Classic" book on the topic- Wonderful introduction to a rich research area- Leading author in the field of algorithmic graph theory- Beautifully written for the new mathematician or computer scientist- Comprehensive treatment

Chapter 1

Graph Theoretic Foundations

Martin Charles Golumbic

Publisher Summary

This chapter presents basic definitions and notations of graph theory. A function that is both injective and surjective is called a bijection. A permutation is simply a bijection from a set to itself. A binary relation R on X may satisfy one or more properties. Such a relation is said to be equivalence if it is reflexive, symmetric, and transitive. A binary relation is called a strict partial order if it is irreflexive and transitive. It is a simple exercise to show that a strict partial order will also be antisymmetric. A graph is defined as a set and a certain relation on that set. It is often convenient to draw a “picture” of the graph. This may be done in many ways. Usually one draws a circle for each vertex and connects vertex x and vertex y with a directed arrow whenever xy is an edge. If both xy and yx are edges, then sometimes a single line joins x and y without arrows.

1 Basic Definitions and Notations

Functions and Relations

Let X and Y be sets. A function (or mapping) f from X to Y, denoted

$f:X\to Y,$

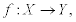
is a rule which associates to each element x of X a corresponding element y of Y. It is usual to call y the image of x under f and denote it by y = f(x). We call f an injective or one-to-one function if no pair of distinct members of X has the same image under f, that is,

$\begin{array}{ll}x\ne x^{\prime }\Rightarrow f\left(x\right)\ne f\left(x^{\prime }\right)\hfill & \left(x,x^{\prime }\in X\right),\hfill \end{array}$

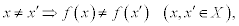
or equivalently,

$\begin{array}{ll}f\left(x\right)=f\left(x^{\prime }\right)\Rightarrow x=x^{\prime }\hfill & \left(x,x^{\prime }\in X\right).\hfill \end{array}$

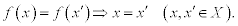
The function f is called surjective or onto if each y in Y is the image of some x in X, that is,

$\begin{array}{lll}\left(\forall y\in Y\right)\left(\exists x\in X\right)\hfill & \text{such that}\hfill & y=f\left(x\right).\hfill \end{array}$

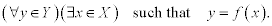
A function which is both injective and surjective is called a bijection. A permutation is simply a bijection from a set to itself.

Following the usual notation of mathematics, x ∈ X indicates that x is a member of the set X and A ⊆ X means that A is a (not n...

Table of contents

• Cover image
• Title page
• Table of Contents
• Copyright page
• Dedication
• Foreword 2004: The annals edition
• Foreword
• Preface
• Acknowledgments
• List of symbols
• Corrections and errata to: Algorithmic graph theory and perfect graphs, the original 1980 edition
• Chapter 1: Graph Theoretic Foundations
• Chapter 2: The Design of Efficient Algorithms
• Chapter 3: Perfect graphs
• Chapter 4: Triangulated graphs
• Chapter 5: Comparability graphs
• Chapter 6: Split graphs
• Chapter 7: Permutation graphs
• Chapter 8: Interval graphs
• Chapter 9: Superperfect graphs
• Chapter 10: Threshold graphs
• Chapter 11: Not So Perfect Graphs
• Chapter 12: Perfect Gaussian Elimination
• Appendix
• Epilogue 2004
• Index