History of Functional Analysis

J. Dieudonne

• Publisher: North Holland
• Year: 1983
• ISBN:
  9780080871608
• Topic: Mathématiques
• Subtopic: Analyse fonctionnelle

History of Functional Analysis presents functional analysis as a rather complex blend of algebra and topology, with its evolution influenced by the development of these two branches of mathematics. The book adopts a narrower definition—one that is assumed to satisfy various algebraic and topological conditions. A moment of reflections shows that this already covers a large part of modern analysis, in particular, the theory of partial differential equations. This volume comprises nine chapters, the first of which focuses on linear differential equations and the Sturm-Liouville problem. The succeeding chapters go on to discuss the ""crypto-integral"" equations, including the Dirichlet principle and the Beer-Neumann method; the equation of vibrating membranes, including the contributions of Poincare and H.A. Schwarz's 1885 paper; and the idea of infinite dimension. Other chapters cover the crucial years and the definition of Hilbert space, including Fredholm's discovery and the contributions of Hilbert; duality and the definition of normed spaces, including the Hahn-Banach theorem and the method of the gliding hump and Baire category; spectral theory after 1900, including the theories and works of F. Riesz, Hilbert, von Neumann, Weyl, and Carleman; locally convex spaces and the theory of distributions; and applications of functional analysis to differential and partial differential equations. This book will be of interest to practitioners in the fields of mathematics and statistics.

Chapter I

Linear Differential Equations and the Sturm-Liouville Problem

§1 Differential Equations and Partial Differential Equations in the XVIII^th Century

Until around 1750, the notion of function of one variable was a very hazy one. The domain where it was defined was very seldom described with precision; it was tacitly assumed that around each point x₀, the function was equal to a power series in x-x₀ and its derivatives were obtained by taking the derivatives of each term of the series. To solve a differential equation of order n

(1)

one would therefore substitute in (1) for y and it’s derivatives a power series

and its derivatives, and identify the series on both sides, which would determine each c_k, for k

n as a function of c_o, c₁,…, c_k−1; the solution thus depended on n arbitrary parameters c₀,…, c_n−1. The very few cases in which it was possible to write explicitly the solution by means of primitives of known functions (such as the linear equation y′ = a(x)y + b(x) of order 1) were already known at the end of the XVII^th century.

After 1760 began the first general study of linear equations of arbitrary order

(2)

D’Alembert observed that the knowledge of a particular solution of the equation and of all solutions of the homogeneous equation L(y) = 0 yields by addition all solutions of (2). A little later, Lagrange [135, vol. I, p. 474] showed that the general solution of L(y) = 0 may be written

where the C_k are arbitrary constants, and the y_k (1

k

n) particular solutions (which he tacitly assumed to be linearly independent). Then, by his famous method of “variation of constants” [135, vol. IV, p. 159], he showed how to obtain also the solutions of (2) when the y_k were known: the solution is written in the form

, where the z_k are unknown functions, subject to n-1 linear relations

(3)

These conditions imply that

for 0

v

n−1; replacing y by

in (2) and using the fact that the y_k satisfy L(y_k) = 0, one obtains for the z’_k another linear equation

(4)

from which, by the Cramer formulas, one can compute the z’_k (1

k

n) and the problem is thus reduced to computing their primitives.

Lagrange also introduced [135, vol. I, p. 471] the notion of adjoint of a linear differential operator L, which was to acquire great importance later: he showed that there exists a linear differential operator M satisfying an identity

(5)

where B is bilinear in (y, y’,…, y⁽ⁿ⁻¹⁾) and (z, z’,…, z⁽ⁿ⁻¹⁾), constituting a generalization of the classical “integration by parts”; he deduced from that formula that if a solution z of M(z) = 0 was known, solutions of L(y) = 0 could be obtained by solving an equation B(y, z) = Const, of order n−1.

Partial differential equations were not considered until the middle of the XVIII^th century, in connection with problems of Mechanics or Physics and then they were of order 2 at least (see §2). The study of partial differential equations of first ord...

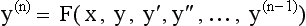
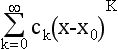
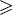
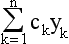
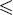
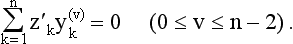
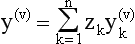
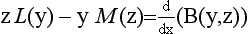
Table of contents

• Cover image
• Title page
• Table of Contents
• Copyright page
• Introduction
• Chapter I: Linear Differential Equations and the Sturm-Liouville Problem
• Chapter II: The “Crypto-Integral” Equations
• Chapter III: The Equation Of Vibrating Membranes
• Chapter IV: The Idea Of Infinite Dimension
• Chapter V: The Crucial Years and the Definition of Hilbert Space
• Chapter VI: Duality and the Definition of Normed Spaces
• Chapter VII: Spectral Theory After 1900
• Chapter VIII: Locally Convex Spaces and the Theory of Distributions
• Chapter IX: Applications of Functional Analysis to Differential and Partial Differential Equations
• References
• Author Index
• Subject Index