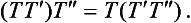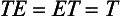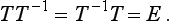Group Theory in Physics

An Introduction

John F. Cornwell

• Publisher: Academic Press
• Year: 1997
• Print ISBN: 9780121898007
• eBook ISBN: 9780080532660
• Topic: Physical Sciences
• Subtopic: Mathematical & Computational Physics

This book, an abridgment of Volumes I and II of the highly respected Group Theory in Physics, presents a carefully constructed introduction to group theory and its applications in physics. The book provides anintroduction to and description of the most important basic ideas and the role that they play in physical problems. The clearly written text contains many pertinent examples that illustrate the topics, even for those with no background in group theory.This work presents important mathematical developments to theoretical physicists in a form that is easy to comprehend and appreciate. Finite groups, Lie groups, Lie algebras, semi-simple Lie algebras, crystallographic point groups and crystallographic space groups, electronic energy bands in solids, atomic physics, symmetry schemes for fundamental particles, and quantum mechanics are all covered in this compact new edition. - Covers both group theory and the theory of Lie algebras - Includes studies of solid state physics, atomic physics, and fundamental particle physics - Contains a comprehensive index - Provides extensive examples

Chapter 1

The Basic Framework

1 The concept of a group

The aim of this chapter is to introduce the idea of a group, to give some physically important examples, and then to indicate immediately how this notion arises naturally in physical problems, and how the related concept of a group representation lies at the heart of the quantum mechanical formulation. With the basic framework established, the next four chapters will explore in more detail the relevant properties of groups and their representations before the application to physical problems is taken up in earnest in Chapter 6.

To mathematicians a group is an object with a very precise meaning. It is a set of elements that must obey four group axioms. On these is based a most elaborate and fascinating theory, not all of which is covered in this book. The development of the theory does not depend on the nature of the elements themselves, but in most physical applications these elements are transformations of one kind or another, which is why T will be used to denote a typical group member.

Definition

Group G

A set G of elements is called a “group” if the following four “group axioms” are satisfied:

(a) There exists an operation which associates with every pair of elements T and T′ of G another element T″ of G. This operation is called multiplication and is written as T″ = TT′, T″ being described as the “product of T with T′“.

(b) For any three elements T, T′ and T″ of G

(1.1)

This is known as the “associative law” for group multiplication. (The interpretation of the left-hand side of Equation (1.1) is that the product TT′ is to be evaluated first, and then multiplied by T″ whereas on the right-hand side T is multiplied by the product T′T″.)

(c) There exists an identity element E which is contained in G such that

for every element T of G.

(d) For each element T of G there exists an inverse element T⁻¹ which is also contained in G such that

This definition covers a diverse range of possibilities, as the following examples indicate.

Example I

The multiplicative group of real numbers

The simplest example (from which the concept of a group was generalized) is the set of all real numbers (excluding zero) with ordinary multiplication as the group multiplication operation. The axioms (a) and (b) are obviously satisfied, the identity is the number 1, and each real number t (≠ 0) has its reciprocal 1/t as its inverse.

Example II

The additive group of real numbers

To demonstrate that the group multiplication operation need not have any connection with ordinary multiplication, take G ...

Table of contents

• Cover image
• Title page
• Table of Contents
• Copyright
• Preface
• Dedication
• Chapter 1: The Basic Framework
• Chapter 2: The Structure of Groups
• Chapter 3: Lie Groups
• Chapter 4: Representations of Groups – Principal Ideas
• Chapter 5: Representations of Groups – Developments
• Chapter 6: Group Theory in Quantum Mechanical Calculations
• Chapter 7: Crystallographic Space Groups
• Chapter 8: The Role of Lie Algebras
• Chapter 9: The Relationships between Lie Groups and Lie Algebras Explored
• Chapter 10: The Three-dimensional Rotation Groups
• Chapter 11: The Structure of Semi-simple Lie Algebras
• Chapter 12: Representations of Semi-simple Lie Algebras
• Chapter 13: Symmetry schemes for the elementary particles
• APPENDICES
• References
• Index