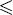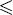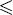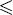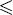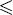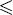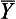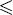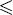Encyclopedia of General Topology

K.P. Hart, Jun-iti Nagata, J.E. Vaughan

• Publisher: Elsevier Science
• Year: 2003
• ISBN:
  9780080530864
• Topic: Mathematics
• Subtopic: Topology
• Index: Mathematics

This book is designed for the reader who wants to get a general view of the terminology of General Topology with minimal time and effort. The reader, whom we assume to have only a rudimentary knowledge of set theory, algebra and analysis, will be able to find what they want if they will properly use the index. However, this book contains very few proofs and the reader who wants to study more systematically will find sufficiently many references in the book.

Key features:

• More terms from General Topology than any other book ever published• Short and informative articles• Authors include the majority of top researchers in the field• Extensive indexing of terms

D

Fairly general properties

d-1

The Low Separation Axioms T₀ and T₁

Karl Heinrich Hofmann, Darmstadt, Germany

A binary relation

on a set is a quasiorder if it is transitive and reflexive. It is called a trivial quasiorder if all-ways x

y, and is defined to be a discrete relation if it agrees with equality; it is said to be an order (sometimes simply called a partial order) if it is antisymmetric, that is, (∀ x, y) ((x

y and y

x) ⇔ (x = y)). A subset Y of a quasiordered set X is a lower set if (∀ x, y) ((x

y and y ∈ Y) ⇒ x ∈ Y); the definition of an upper set is analogous. On a topological space X set x

y iff every neighbourhood of x is a neighbourhood of y. This definition introduces a quasiorder

, called the specialisation quasiorder of X. The terminology originates from algebraic geometry, see [18, II, p. 23]. The specialisation quasiorder is trivial iff X has the indiscrete topology. The closure

of a subset Y of a topological space X is precisely the lower set ↓ Y of all x ∈ X with x

y for some y ∈ Y. The singleton closure {

} is the lower set ↓ {x}, succinctly written ↓ x. The intersection of all neighbourhoods of x is the upper set ↑ x = {y ∈ X : x

y}.

A topological space X is said to satisfy the separation axiom T₀ (or to be a T₀-space), and its topology

_X is called a T₀-topology, if the specialisation quasiorder is an order; in this case it is called the specialisation order. The space X is said to satisfy the separation axiom T₁ (or to be a T₁-space), and its topology

_X is called a T₁-topology, if the specialisation quasiorder is discrete. The terminology for the hierarchy T_n of separation axioms appears to have entered the literature 1935 through the influential book by Alexandroff and Hopf [3] in a section of the book called “Trennungsaxiome” (pp. 58 ff.). A space is a T₀-space iff

(0) for two different points there is an open set containing precisely one of the two points,

and it is a T₁-space iff

(1) every singleton subset is closed.

Alexandroff and Hopf call postulate (0) “das nullte Kolmogoroffsche Trennungsaxiom” and postulate (1) “das er-ste Frechetsche Trennungsaxiom” [3, pp. 58, 59], and they attach with the higher separation axioms the names of Hausdorff, Vietoris and Tietze. In Bourbaki [4], T₀-spaces are relegated to the exercises and are called

espaces de Kolmogoroff

(see § 1, Ex. 2, p. 89). Alexandroff and Hopf appear to have had access to an unpublished manuscript by Kolmogoroff which appears to have dealt with quotient spaces [3, pp. 61, 619]. It is likely to have been the origin of this terminology to which Alexandroff continues to refer in later papers (see, e.g., [2]). Fréchet calls T₁-spaces

espaces accessibles

[7, p. 185]. From an axiomatic viewpoint, the postulate (1) is a natural separation axiom for those who base topology on the concept of a closure operator (Kuratowski 1933); Hausdorff’s axiom, called T₂ by Alexandroff and Hopf, is a natural one if the primitive concept is that of neighbourhood systems (Hausdorff [9] 1914). In [14] Kuratowski joins the...