Space, Time and Number in the Brain

Searching for the Foundations of Mathematical Thought

Stanislas Dehaene, Elizabeth Brannon

• Publisher: Academic Press
• Year: 2011
• Print ISBN: 9780123859488
• eBook ISBN: 9780123859495
• Topic: Psicología
• Subtopic: Psicología cognitiva y cognición

The study of mathematical cognition and the ways in which the ideas of space, time and number are encoded in brain circuitry has become a fundamental issue for neuroscience. How such encoding differs across cultures and educational level is of further interest in education and neuropsychology. This rapidly expanding field of research is overdue for an interdisciplinary volume such as this, which deals with the neurological and psychological foundations of human numeric capacity. A uniquely integrative work, this volume provides a much needed compilation of primary source material to researchers from basic neuroscience, psychology, developmental science, neuroimaging, neuropsychology and theoretical biology.- The first comprehensive and authoritative volume dealing with neurological and psychological foundations of mathematical cognition- Uniquely integrative volume at the frontier of a rapidly expanding interdisciplinary field- Features outstanding and truly international scholarship, with chapters written by leading experts in a variety of fields

Chapter 1. Mental Magnitudes

C.R. Gallistel

Department of Psychology and Rutgers Center for Cognitive Science, Rutgers University, New Brunswick, USA

Summary

Mental magnitudes are physically realized symbols in the brain. They refer to continuous and discrete quantities an animal has experienced, and they enter into arithmetic processing. Arithmetic is special because of its extraordinary representational power. The processing machinery is strongly constrained by both referential and computational considerations.

As is evident from the other chapters in this volume, the experimental study of the mind’s foundational abstractions has become an important part of cognitive science. Prominent among those abstractions are space, time, number, rate and probability, which have now been shown to play a fundamental role in the mentation of nonverbal animals and preverbal humans [1], [2], [3], [4] and [5]. The results have moved cognitive science in a rationalist direction. In an empiricist theory of mind, these concepts are somehow induced from primitive sensory experience. Because language has often been thought to mediate the induction, these abstractions were often supposed to be absent in the mentation of nonverbal or preverbal beings. In a rationalist epistemology, by contrast, these abstractions are foundational. They make sensory experience possible. I suggest that the brain’s ability to represent these foundational abstractions depends on a still-more basic ability, the ability to store, retrieve and arithmetically manipulate signed magnitudes [6]. If this is true, then the discovery of the physical basis of this ability is a sine qua non for a well-founded cognitive neuroscience.

By magnitude I mean computable number, a magnitude that can be subjected to arithmetic manipulation in a physically realized system (see Box 1.1). I use ‘magnitude’ to avoid confusions that arise from ‘number’. ‘Number’ may denote the numerosity of a set, or it may denote the symbols in a system of arithmetic, which may or may not refer to numerosities. The symbol ‘1’ may denote the numerosity of a set, or the height in meters of a large dog, or the multiplicative identity element in the system of arithmetic.

Box 1.1
Why Arithmetic is Special

Eugene Wigner [20] called attention to “The unreasonable efficacy of mathematics in the natural sciences.” Mathematics rests on arithmetic. Representations constructed on this simple foundation have proved surprisingly successful in representing the natural world. Based on ethnographic and psychological evidence, Fiske has argued that humans, at least, also use mental magnitudes to represent the social world [21]. Box 1.1 Fig. 1 reminds the reader of the ways in which magnitudes may be used to represent space, time, number, probability, and rate. It uses the lengths of lines in place of number symbols, because length instantiates magnitude.

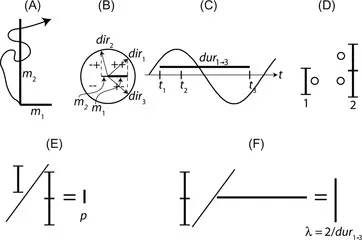Box 1.1 Figure 1 (A) The representation or location in two or three dimensions, as in dead reckoning while foraging (trace ending in location arrow), may be mediated by a vector composed of two or three magnitudes (m1 & m2). (B) The representation of direction, which is critical in dead reckoning, may be reduced to a magnitude proportional to the cosine of the direction angle and two signs. The signs code the quadrant. The magnitude codes direction within it: dir1 is encoded by 〈m1,+,+〉, dir2 by 〈m2,−,+〉 and dir3 by 〈m1,+,−〉. (C) Durations are represented by single magnitudes (dur1→3), which may be computed from differences in temporal locations (t1,t2,t3): dur1→3=t3−t1. Temporal locations may be represented by the phases of endogenous clocks, like the circadian clock [22] and phase may be represented in the same way as directions: 〈m1,+,+〉, 〈m2,−,+〉 and 〈m1,+,−〉 could represent t1,t2,t3 as readily as dir1, dir2, and dir3. (D) Numerosity is also represented by analog-like magnitudes [23]. (E) Dividing magnitudes representing numerosity (discrete quantity) generates magnitudes representing probability and proportion (continuous quantities). (F) Dividing magnitudes representing numerosity by magnitudes representing duration yields magnitudes representing rates.

The representations shown are conventional and elementary. The brain’s representations are likely more sophisticated, hence less transparent. See, for example, Chapter 5 in this volume. Nonetheless, they, like those portrayed here, must enable arithmetic processing to be brought to bear in behaviorally useful ways. What makes arithmetic special is its representational power.

I begin with a short review of some of the behaviorally implied representations that would seem to be constructed from mental magnitudes, emphasizing the basic computational operations that appear to be performed on them. This leads me to consider the constraints this usage would impose on the system of mental magnitudes. One constraint is that mental magnitudes must cover a huge range. Logarithmic mappings from real-world magnitudes to mental magnitudes would be one way of accomplishing this, but such a mapping leads to computational problems. I suggest an alternative: autoscaling. I then argue that one constraint links a computational role to a referential role: the mental magnitude that functions as the multiplicative identity in the brain’s computations must refer to numerosity one in the mapping from discrete quantity (numerosity) to mental magnitudes. I conclude that the properties of mental magnitudes are strongly constrained, not just by their reference, but also by the computational considerations. Awareness of these constraints can focus neurobiological inquiry.

Computational Implications of Behavioral Results

The representation of space arises in its most basic form in the process of dead reckoning (aka path integration), which is the foundation of an animal’s ability to find its way back whence it came and to construct a representation of the locations of landscapes and locations relative to a home base [2]. It requires summing successive displacements in a framework in which the coordinates of locations other than that of the animal do not change as the animal moves. By summing successive small displacements (small changes in its location), the animal maintains a representation of its location. This representation makes it possible to record locations of places and objects of interest as it encounters them, thereby constructing a cognitive map of the experienced environment. Computational considerations make it likely that this representation is Cartesian and allocentric. Polar and egocentric representations rapidly become inaccurate, because they integrate the step-by-step errors in the signals for the direction and distance of displacements in such a way that the inaccuracy of each step in the integration is increased by inaccuracies incorporated at earlier steps [2].

The representations of locations are vectors, ordered sets of magnitudes. A fundamental operation in navigation is computing courses—the range and bearing of a destination from the current location. If the vectors are Cartesian, the range and bearing are the modulus and angle of the difference between the destination vector and the current–location vector. This difference is the element-by-element differences between the two vectors. Thus, putting a representation of spatial location to use in navigational computations depends on the arithmetic processing of the magnitudes that constitute the vector.

The representation of time takes two forms: the representation of phase (location within one or more cycles) and the representation of temporal intervals. Nonverbal animals represent both [2] and they compute signed temporal differences: how long it will be, and how long it has been. A behavioral manifestation of the first computation (how long it will be) is the anticipation of time of feeding seen when animals are fed at regular times of day (for review, see [2]). A behavioral manifestation of the latter is the cache-revisiting behavior of scrub jays: their choice of which caches to visit first depends on their knowledge of how long it has been since they buried what where and on their acquired knowledge of the (experimenter-determined) rotting-times for the different foods they have cached [7].

It has been widely supposed that the representation of temporal intervals is generated by an interval-timing mechanism [8]. There is a conceptual problem with this hypothesis: the ability to record the first occurrence of an interesting temporal interval would seem to require the starting of an infinite number of timers for each of the very large number of experienced events that might turn out to be the start of something interes...

Table of contents

• Cover image
• Table of Contents
• Front-matter
• Copyright
• Contributors
• Foreword
• Section I Mental Magnitudes and their Transformations
• Chapter 1. Mental Magnitudes
• Chapter 2. Objects, Sets, and Ensembles
• Chapter 3. Attention Mechanisms for Counting in Stabilized and in Dynamic Displays
• Section II Neural Codes for Space, Time and Number
• Chapter 4. A Manifold of Spatial Maps in the Brain*
• Chapter 5. Temporal Neuronal Oscillations can Produce Spatial Phase Codes
• Chapter 6. Population Clocks
• Chapter 7. Discrete Neuroanatomical Substrates for Generating and Updating Temporal Expectations
• Chapter 8. The Neural Code for Number
• Section III Shared Mechanisms for Space, Time and Number?
• Chapter 9. Synesthesia
• Chapter 10. How is Number Associated with Space? The Role of Working Memory
• Chapter 11. Neglect “Around the Clock”
• Chapter 12. Saccades Compress Space, Time, and Number*
• Section IV Origins of Proto-Mathematical Intuitions
• Chapter 13. Origins of Spatial, Temporal, and Numerical Cognition
• Chapter 14. Evolutionary Foundations of the Approximate Number System
• Chapter 15. Origins and Development of Generalized Magnitude Representation
• Section V Representational Change and Education
• Chapter 16. Foundational Numerical Capacities and the Origins of Dyscalculia*
• Chapter 17. Neurocognitive Start-Up Tools for Symbolic Number Representations*
• Chapter 18. Natural Number and Natural Geometry
• Chapter 19. Geometry as a Universal Mental Construction
• Chapter 20. How Languages Construct Time
• Chapter 21. Improving Low-Income Children’s Number Sense
• Index