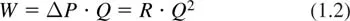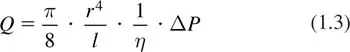Microcirculation

Ronald F. Tuma, Walter N. Duran, Klaus Ley

• Publisher: Academic Press
• Year: 2011
• ISBN:
  9780080569932
• Edition: 2
• Topic: Ciencias biológicas
• Subtopic: Fisiología

This reference is a volume in the Handbook of Physiology, co-published with The American Physiological Society. Growth in knowledge about the microcirculation has been explosive with the field becoming fragmented into numerous subdisciplines and subspecialties. This volume pulls all of the critical information into one volume.

• Meticulously edited and reviewed. Benefit: Provides investigators a unique tool to explore the significance of their findings in the context of other aspects of the microcirculation. In this way, the updated edition has a direct role in helping to develop new pathways of research and scholarship
• Highlights the explosive growth in knowledge about the microcirculation including the biology of nitric oxide synthase (NOS), endothelial cell signaling, angiogenesis, cell adhesion molecules, lymphocyte trafficking, ion channels and receptors, and propagated vasomotor responses. Benefit: Microcirculatory biology has become fragmented into numerous sub-disciplines and subspecialties, and these reference reintegrates the information in one volume

Chapter 1
Blood Flow in Microvascular Networks

Axel R Pries^1,2 and Timothy W Secomb³

¹ Department of Physiology, Charité Berlin CBF, Arnimallee, Berlin, Germany
² German Heart Center Berlin, Augustenburger Platz, Berlin, Germany
³ Department of Physiology, University of Arizona, Tucson, AZ, USA

1.1 Introduction

1.2 Flow in single microvessels

1.2.1 Flow resistance, Poiseuille’s law, and effective viscosity

1.2.2 Fåhraeus effect

1.2.3 Fåhraeus–Lindqvist effect

1.2.4 Aggregation and sedimentation

1.2.5 Endothelial surface layer

1.2.6 Effective blood viscosity in vivo

1.3 Microvascular networks

1.3.1 General features

1.3.2 Topology

1.3.3 Topological growth models

1.3.4 Segment lengths and diameters

1.3.5 Heterogeneity and correlations

1.3.6 Flow and transit time

1.3.7 Pressure and wall stresses

1.3.8 Phase separation in bifurcations

1.3.9 Network Fåhraeus effect

1.4 Relationship of network structure and flow to physiological functions

1.4.1 Transport functions

1.4.2 Inflammatory and immune functions

1.4.3 Regulation of blood flow

1.4.4 Structural adaptation

1.5 Conclusions

References

1.1 INTRODUCTION

Terminal vascular beds bring flowing blood into close proximity with parenchymal cells. The need for adequate exchange of materials between blood and tissue, and particularly for oxygen delivery, is met by large numbers of closely spaced microvessels with small diameters and large cumulative surface area, interconnected in intricate network structures. The flow of blood through such microvascular networks is the subject of the present chapter, with emphasis on biophysical aspects.

Blood is a suspension containing a high volume fraction of red blood cells (erythrocytes) and other suspended elements. Red blood cells increase the oxygen carrying capacity of blood, which would otherwise be relatively small because the solubility of oxygen in water is low. With a volume fraction (hematocrit) typically about 45%, red blood cells exert a large influence on the flow properties of blood. Other suspended elements, including white blood cells (leukocytes) and platelets, have critical biological roles but are normally present at much lower volume fractions and therefore have less effect on flow properties.

The diameters of blood vessels forming the microcirculation range from a few hundred microns down to a few microns, while the diameter of a freely suspended human red blood cell is about 8 μm. Consideration of blood flow in microvessels must therefore take into account the particulate nature of blood and the finite dimensions of red blood cells. This contrasts with the situation in larger blood vessels, where blood can generally be considered as a continuous material (a continuum) whose physical behavior is adequately described in terms of bulk properties such as viscosity. Microvessels are lined by endothelial cells that present a specialized surface to flowing blood. Attached to the luminal face of the endothelial cells is the endothelial surface layer (ESL), a relatively thick (0.5–1 micron or more) layer of macromolecules which has significant impact on blood flow. The effects on blood flow of these features of microvessels are described in Section 1.2.

In order to supply all tissue cells in a given organ volume, the exchange vessels of a microvascular network must form a space-filling mesh. The vessels supplying and draining the network are embedded in the tissue or attached to its surface. These conditions imply large heterogeneity in path length and number of vessel segments between the main vessels and the terminal branches. The uneven partition of red blood cell and plasma flows at diverging branch points (bifurcations) in the network structure results in heterogeneous vessel hematocrit. Thus, microvascular networks cannot be considered as simple serial arrangements of different vessel classes (e.g., capillaries, terminal arterioles) consisting of large numbers of parallel identical vessels. The relationship between the distribution of structural and functional parameters in such networks, which is crucial for adequate distribution of blood flow, is described in Section 1.3.

The last section presents a discussion of the relationship of network structure and flow to physiological aspects of the microvasculature including transport functions, inflammatory and immune functions, regulation of blood flow, and structural adaptation.

1.2 FLOW IN SINGLE MICROVESSELS

1.2.1 Flow resistance, Poiseuille’s law, and effective viscosity

Flow in blood vessels is driven primarily by the hydrostatic pressure generated by the beating heart. The relationship between rate of flow and the driving pressure, whether of a single vascular segment or of the entire peripheral circulation, is conveniently expressed in terms of the flow resistance, R:

where ΔP is the pressure difference driving the flow and Q is the volume flow rate. The flow resistance determines the pressure required to sustain a given flow rate, and the rate of work that must be done, which is given by

Within a network of vessels, the distribution of flow and pressure drop is determined by the distribution of resistance, according to rules analogous to those applying to networks of electrical resistances. In a set of parallel flow pathways subjected to a given pressure drop, for example, the flow in each pathway is inversely proportional to the flow resistance of that pathway. In a flow pathway consisting of several elements in series, all carrying the same flow, the pressure drop across each element is linearly proportional to the flow resistance of that element. Knowledge of the factors determining the flow resistance of vessel segments is therefore important in understanding the distribution of blood flow in the circulatory system.

In the third decade of the nineteenth century, Jean-Louis-Marie Poiseuille performed direct measurements of arterial and venous blood pressure [1, 2] and found high pressure in arterial and low pressures in venous vessels irrespective of the size of vessel. From these results, he concluded that the pressure drop in the circulation must occur mainly in the peripheral vascular beds. Direct pressure measurements in the small vessels of the microcirculation were not feasible at that time, or indeed for another 100 years [3]. Instead, Poiseuille investigated the passage of simple fluids through long, narrow-bore tubes [4, 5] to indirectly investigate the source of flow resistance in the circulation.

The main findings of Poiseuille’s meticulous work can be represented by the equation, which was actually derived later but is generally known as Poiseuille’s Law:

This equation gives the flow (Q) through a cylindrical tube as a function of the driving pressure difference along the tube (ΔP), the tube radius (r) and length (l). The dynamic viscosity (η) is a material property of the fluid which describes its internal resistance to shearing motions, in which different parts of the fluid move with different velocities. With respect to the distribution of blood pressure and flow in the circulation, an important consequence is the relation between flow resistance and vessel radius:

Flow resistance in individual vessels increases very sharply with decreasing vessel diameter.

The derivation of Poiseuille’s law depends on a number of assumptions. The tube is assumed to be uniform with a circular cross section. The flow is assumed to be steady (unvarying in time) and laminar (free of turbulence), and the fluid is assumed to be Newtonian, with a fixed viscosity. In practice, all these conditions are rarely if ever satisfied in the circulatory system. Nonetheless, Poiseuille’s law is often a useful approximation and represents a logical starting point for any analysis of blood flow in microvessels. The Reynolds number of blood flowing in microvessels is generally in the range 10^–3 to about 1. Therefore, the flow is laminar. Effects of fluid inertia may be neglected in many cases, particularly in smaller microvessels.

Formal derivations of Poiseuille’s law are given in several texts (e.g. [6]). The dependence of flow rate on tube radius according to eq. (1....

Table of contents

• Cover
• Copyright
• Contributors
• Preface
• Introduction Overview of the Microcirculation
• Chapter 1 Blood Flow in Microvascular Networks
• Chapter 2 Physiology and Pathobiology of Microvascular Endothelium
• Chapter 3 Biology of Nitric Oxide Synthases
• Chapter 4 Microcirculatory Exchange Function
• Chapter 5 Microlymphatic Biology
• Chapter 6 Local Regulation of Microvascular Perfusion
• Chapter 7 Receptor-Mediated Events in the Microcirculation
• Chapter 8 Angiogenesis
• Chapter 9 The Microcirculation in Inflammation
• Chapter 10 Lymphocyte Trafficking
• Chapter 11 The Cerebral Microcirculation
• Chapter 12 Regulation of Coronary Microvascular Resistance in Health and Disease
• Chapter 13 The Renal Microcirculation
• Chapter 14 Gastrointestinal and Liver Microcirculations: Roles in Inflammation and Immunity
• Chapter 15 The Pulmonary Microcirculation
• Chapter 16 Microcirculation of the Ocular Fundus
• Chapter 17 Sickle Cell Disease
• Chapter 18 Pathophysiology of Primary Hypertension
• Chapter 19 Microvascular Consequences of Obesity and Diabetes
• Index