Unified Constitutive Laws of Plastic Deformation

A. S. Krausz, K. Krausz

• Publisher: Academic Press
• Year: 1996
• Print ISBN: 9780124259706
• eBook ISBN: 9780080543437
• Topic: Technology & Engineering
• Subtopic: Zoology
• Index: Technology & Engineering

High-technology industries using plastic deformation demand soundly-based economical decisions in manufacturing design and product testing, and the unified constitutive laws of plastic deformation give researchers aguideline to use in making these decisions. This book provides extensive guidance in low cost manufacturing without the loss of product quality. Each highly detailed chapter of Unified Constitutive Laws of Plastic Deformation focuses on a distinct set of defining equations. Topics covered include anisotropic and viscoplastic flow, and the overall kinetics and thermodynamics of deformation. This important book deals with a prime topic in materials science and engineering, and will be of great use toboth researchers and graduate students. - Describes the theory and applications of the constitutive law of plastic deformation for materials testing - Examines the constitutive law of plastic deformation as it applies to process and product design - Includes a program on disk for the determination and development of the constitutive law of plastic deformation - Considers economical design and testing methods

1

Unified Cyclic Viscoplastic Constitutive Equations: Development, Capabilities, and Thermodynamic Framework

J.L. Chaboche, ONERA 92320 Chatillon, France

LIST OF SYMBOLS

General notation:

X scalar functions, parameters, or variables

X second-or fourth-rank tensors

X’ deviator of the second-rank tensor X

· scalar product of vectors or contracted tensor product

: tensorial product contracted twice

tensorial products

||X||_M generalized second invariant of X : ||X||_M = (X : M : X)^1/2

time derivative of a

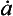
∂/∂x partial derivative

d/dx total derivative

δ Kroenecker delta

I fourth-rank unity tensor

I_dev fourth-rank deviatoric operator

Specific variables or functions:

α “back strain” or state variable associated with back stress

a aging state variable

δ isotropic “drag” state variable

D drag stress

ε strain tensor

ε_e elastic strain tensor

ε_p plastic strain or viscoplastic strain tensor

Ψ thermodynamic state potential

ϕ dissipation potential (rates)

^* dual dissipation potential (forces)

ϕ dissipation

f yield function

h hardening modulus

J, J_T second invariant overstress and back stress

plastic multiplier

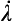
λ elastic stiffness tensor

n direction of plastic flow

ν direction of the back-stress rate

Ω, Ω_p viscoplastic potential

Ω_r static recovery potential

p accumulated plastic strain

q heat flux vector

r isotropic “yield“ state variable

R yield stress increase

S entropy

σ, σ’ stress tensor, stress deviator

T temperature

∇T temperature gradient

u internal energy

W_p plastic work

W_s stored energy

X, X’ back stress tensor and its deviator

Y yield stress

Z thermodynamic force associated with aging variable a

I INTRODUCTION

The constitutive equations considered here, mainly those devoted to metallic materials, are essentially developed with the objective of the inelastic analysis of structural components. Initially, they are based on the concepts of continuum mechanics, where a particular representative volume element of material can be considered as submitted to a macroscopically uniform stress, neglecting the microstress/microstrain inhomogeneities at the microscale (but not their effects).

The physical facts, the precise role of the dislocations, their arrangements, and their evolution are considered more in detail in several other chapters of this book. Here, we concentrate on a macroscopic description of the various processes, making reference to the microstructural events as often as possible (at least qualitatively).

The application domains are limited to the quasistatic deformation of metallic materials (strain rate between 10⁻¹⁰ and 10⁻¹), especially under cyclic loading conditions. The constitutive equations are written in their small strain form. Also, high-temperature conditions will be considered, as well as loading under varying temperatures.

By “unified viscoplastic constitutive equations,” we mean the nonseparation of the plastic (rate-independent) and creep (rate-dependent) parts of the inelastic strain. Moreover, the considered viscoplastic equations are based on a general framework consistent both with classical plasticity (elastic domain, yield surface, loading/unloading condition) and with thermoviscoplasticity without an elastic domain. Then rate-independent conditions will be obtained consistently as a limit case of the general viscoplastic scheme.

The theoretical development of viscoplasticity has its origin in the works of Bingham and Green (1919), Hohenemser and von Prager (1932), Oldroyd (1947), Malvern (1951), Odqvist (1953), Stowell (1957), and Prager (1961), whose models do not contain evolving internal stage variables. The field started to gain momentum in the mid-1960s when internal state variable models began to appear in the theories of Perzyna (1964) and Armstrong and Frederick (1966). With the increased availability of the computer, rapid advances were made in the 1970s through t...

Table of contents

• Cover image
• Title page
• Table of Contents
• Copyright
• Contributors
• Preface
• Chapter 1: Unified Cyclic Viscoplastic Constitutive Equations: Development, Capabilities, and Thermodynamic Framework
• Chapter 2: Dislocation-Density–Related Constitutive Modeling
• Chapter 3: Constitutive Laws for High-Temperature Creep and Creep Fracture
• Chapter 4: Improvements in the MATMOD Equations for Modeling Solute Effects and Yield-Surface Distortion
• Chapter 5: The Constitutive Law of Deformation Kinetics
• Chapter 6: A Small-Strain Viscoplasticity Theory Based on Overstress
• Chapter 7: Anisotropic and Inhomogeneous Plastic Deformation of Polycrystalline Solids
• Chapter 8: Modeling the Role of Dislocation Substructure during Class M and Exponential Creep
• Chapter 9: Comments and Summary
• Index