Philosophical Logic

A Contemporary Introduction

John MacFarlane

• Publisher: Routledge
• Year: 2020
• Print ISBN: 9781138737655
• eBook ISBN: 9781351733557
• Topic: Computer Science
• Subtopic: Teaching Arts & Humanities
• Index: Computer Science

Introductory logic is generally taught as a straightforward technical discipline. In this book, John MacFarlane helps the reader think about the limitations of, presuppositions of, and alternatives to classical first-order predicate logic, making this an ideal introduction to philosophical logic for any student who already has completed an introductory logic course.

The book explores the following questions. Are there quantificational idioms that cannot be expressed with the familiar universal and existential quantifiers? How can logic be extended to capture modal notions like necessity and obligation? Does the material conditional adequately capture the meaning of 'if'—and if not, what are the alternatives? Should logical consequence be understood in terms of models or in terms of proofs? Can one intelligibly question the validity of basic logical principles like Modus Ponens or Double Negation Elimination? Is the fact that classical logic validates the inference from a contradiction to anything a flaw, and if so, how can logic be modified to repair it? How, exactly, is logic related to reasoning? Must classical logic be revised in order to be applied to vague language, and if so how? Each chapter is organized around suggested readings and includes exercises designed to deepen the reader's understanding.

Key Features:

• An integrated treatment of the technical and philosophical issues comprising philosophical logic
• Designed to serve students taking only one course in logic beyond the introductory level
• Provides tools and concepts necessary to understand work in many areas of analytic philosophy
• Includes exercises, suggested readings, and suggestions for further exploration in each chapter

1 Fundamentals

Fundamentals. A concise review of propositional logic and first-order predicate logic with identity, covering syntax, semantics, Fitch-style natural deductions, and basic concepts.

In general, the task of describing a logical system comes in three parts:

Grammar Describing what counts as a formula.

Semantics Defining truth in a model (and, derivatively, logical consequence and related notions).

Proofs Describing what counts as a proof.

In this chapter, we will go through these three parts for propositional logic, predicate logic, and the logic of identity. We will also review the distinction between use and mention and introduce Quine’s device of “quasiquotation,” which we will need later to keep from getting confused.

We assume you have taken a first course in symbolic logic, covering propositional and predicate logic (but not metalogical results like soundness and completeness). But, because such courses differ considerably in the symbols, terminology, and proof system they use, a brief review of these fundamentals will help ensure that everyone is on the same page with the basics.

Some or all of this may be old hat. Other things may be unfamiliar. Many logic textbooks do not give a rigorous account of the semantics of first-order logic, and many do not teach the Fitch-style natural deduction proofs used here. Sometimes courses in predicate logic do not cover identity at all. Before going further in this book, you should be comfortable doing exercises of the sort given in this chapter.

1.1 Propositional logic

1.1.1 Grammar

• A propositional constant (a capital letter, possibly with a numerical subscript) is a formula. There are infinitely many propositional constants: A, B₁₅, Z₇₃₁, etc.

• ⊥ is a formula.

• If p and q are formulas, then (p ∨ q), (p ∧ q), (p ⊃ q), (p ≡ q), and ¬p are formulas.

• Nothing else is a formula.

You might have used different symbols in your logic class: & or • for conjunction, ∼ or • for negation, → for the conditional, ↔ for the biconditional. You might not have seen ⊥ (called bottom, falsum, or das Absurde): we will explain its meaning shortly.

The lowercase letters p and q are not propositional constants. They are used to mark places where an arbitrary formula may be inserted into a schema: a pattern that many different formulas can “fit” or “instantiate.” Here are some instances of the schema (p ∧ (p ∨ qq)):

(1)

(2)

In (1), we substituted the formula (A ∧ B) for the letter p in the schema, and we substituted the formula ¬A for q. In (2), we substituted (A ∨ ¬B) for both p and q. Can you see why the following formulas are not instances of (p ∧ (p ∨ q))?

(3) (A∧ (B ∨ C))

(4) (¬ A∧ (¬A ∨ B))

Convention for parentheses. The parentheses can get a bit bothersome, so we will adopt the following conventions:

• Outer parentheses may be dropped: so, for example, A ∨B is an abbreviation for (A ∨ B). • We will consider (p ∨ q ∨ r) as an abbreviation for ((p ∨ q) ∨ r), and (p ∧ q ∧ r) as an abbreviation for ((p ∧ q) ∧ r)

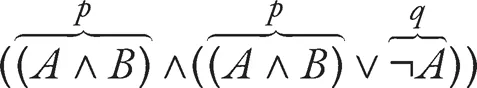
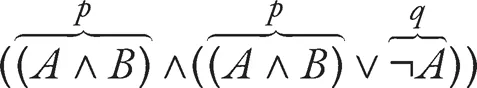
1.1.2 Semantics

Logicians don’t normally concern themselves much with truth simpliciter. Instead, they use a relativized notion of truth: truth in a model. You may not be familiar with this terminology, but you should be acquainted with the idea of truth in a row of a truth table, and in (classical) propositional logic, that is basically what truth in a model amounts to.

A model is something that provides enough information to determine truth values for all of the formulas in a language. How much information is required depends on the language. In the simple propositional language we’re considering, we have a very limited vocabulary—propositional constants and a few truth-functional connectives—and that allows us to use very simple models. When we add quantifiers, a...

Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Table of Contents
• List of Exercises
• Preface
• Acknowledgements
• 1 Fundamentals
• 2 Quantifiers
• 3 Modal Logic
• 4 Conditionals
• 5 Logical Consequence via Models
• 6 Logical Consequence via Proofs
• 7 Relevance, Logic, and Reasoning
• 8 Vagueness and the Sorites Paradox
• Appendix A Greek Letters
• Appendix B Set-Theoretic Notation
• Appendix C Proving Unrepresentability
• References
• Index