Scaling the Secular City

A Defense of Christianity

J. P. Moreland

• Publisher: Baker Academic
• Year: 1987
• Print ISBN: 9780801062223
• eBook ISBN: 9781585580712
• Topic: Theology & Religion
• Subtopic: Christian Ministry

This volume offers up-to-date arguments for God's existence and for Jesus's deity and resurrection, answers to objections to Christian theism, and discussions of four key issues.

1

---

The Cosmological Argument

Forms of the Argument

The Thomist Argument

The Leibnizian Argument

The Kalam Argument

Statement of the Kalam Argument

Overview

Set Theory

Actual Infinity

Potential Infinity

Defense of the Kalam Argument

Premise 1: The Universe Had a Beginning

The Nonexistence of an Actual Infinite

Puzzles with an Actual Infinite

Three Objections to the Puzzles

The Impossibility of Traversing an Actual Infinite

Statement and Support of the Argument

Objections to the Argument

The Big Bang Cosmology

The Second Law of Thermodynamics

The Argument

Two Objections

Premise 2: The Beginning of the Universe Was Caused

Premise 3: The Cause for the Beginning of the Universe Was Personal

One of the most important arguments for God’s existence is the cosmological argument. It has had a tarnished yet sturdy history and, like the Bible, it has outlived most of its critics. The argument gets its name from the Greek word kosmos, which means “world” or “universe.” The argument generally begins with the existence of the world or some part of it and seeks to establish the existence of a necessary Being who causes the existence of the world.

Actually, there are three very different forms of the cosmological argument. This is important to keep in mind, since in many cases critics will raise what they believe to be objections against the cosmological argument in general. Their objections, even if successful, often work against only one form of the argument.

The three forms of the cosmological argument are the Thomist argument, the Leibnizian argument, and the kalam argument. Since the main burden of this chapter is to state and defend the kalam cosmological argument, I will mention only briefly the other two forms. This is not to imply they are not valuable. Both of them are good arguments. But the kalam argument has not received the attention it deserves, so this chapter will center on stating and defending it.

The Thomist Argument

The Thomist argument receives its name from Saint Thomas Aquinas (1225–1274). It begins by asserting the existence of finite, contingent beings. These would be beings which could have not existed and thus are dependent for their being on something else. Finite beings owe their current existence either to an infinite regress of other dependent beings or to a necessary Being, one which could not cease to exist if it does in fact have existence. An infinite regress of finite beings does not cause the existence of anything.[1] Adding another dependent being to a chain of dependent beings does not ground the existence of the chain. To say that it does is like saying one could get an orange by adding an infinite number of apples to a basket of apples. Adding apples to apples does not yield an orange; adding dependent beings to dependent beings does not yield a necessary Being. The current existence of all finite beings is caused or grounded by the existence of a necessary Being, and this being is God.

Three features of the argument are central. First, proponents must spell out what it is to be a dependent being; this is done by appealing to what is called the essence/existence distinction. A being’s essence is its whatness or nature and its existence is its thatness (that it is). Proponents argue that one cannot move from a finite thing’s essence to its existence. By contemplating Fido’s dogness it does not follow that Fido really exists. If he does exist, being must be given to his essence.

Second, the nature of the infinite regress used in the argument is important. The regress of beings does not go back through time, but is current or simultaneous. Third, the nature of God as a necessary Being is crucial. God is necessary in a metaphysical sense. This is sometimes put by saying that God is necessary de re. It is not a logical contradiction to deny God’s existence. Rather, if God exists he exists necessarily. He could not have not-existed.

There are a number of contemporary advocates of the Thomist argument. Two of them are Norman L. Geisler and Bruce R. Reichenbach.[2]

The Leibnizian Argument

The Leibnizian cosmological argument receives its name from the philosopher Gottfried Wilhelm Leibniz (1646–1716). It begins by asking the question “why is there something rather than nothing?” Why does anything at all exist? It then uses the principle of sufficient reason (for anything that exists, there must be some reason, some purpose or rational context, why it exists rather than not exists) to argue for the existence of an intrinsically intelligible or self-explanatory being—God—whose existence is logically necessary. This is sometimes put by saying that God’s existence is necessary de dicto. That is, it would be a logical contradiction to deny the proposition God exists.[3]

Two issues are important for this argument. First, why should anyone believe in the principle of sufficient reason? It may hold on a limited basis. For example, if I take my car to the garage to have it fixed, I would certainly think it odd for the mechanic to tell me that there is no reason why it does not work. He may not know the reason, but surely there is one. But does the principle hold with regard to the universe as a whole? Could not one agree with atheist Bertrand Russell and simply say that the universe is just there and that is all? There is no explanation. I do not find Russell’s response satisfying, but in any case, the principle of sufficient reason, at least as it applies to the universe as a whole, is a key issue in the Leibnizian argument.

The second important issue involves whether or not any being’s existence is logically necessary. Is it a contradiction to deny the existence of any being? Deciding this question requires, among other things, a discussion of the ontological argument and its relationship to the cosmological argument. A recent proponent of this form of the cosmological argument is Richard Taylor.[4]

The Kalam Argument

The kalam cosmological argument gets its name from the word kalam, which refers to Arabic philosophy or theology. The kalam argument was popular among Arabic philosophers in the late Middle Ages. Christian philosophers during that period did not generally accept the argument, perhaps due to the influence of Aquinas, who, following Aristotle, rejected it.[5] A notable exception was Saint Bonaventure, a contemporary of Aquinas, who argued extensively for the soundness of the kalam argument.[6]

In recent years, there has been a small but growing number of thinkers who have defended this line of reasoning.[7] But without doubt, the most thorough and articulate advocate of the argument has been William Lane Craig.[8]

Statement of the Kalam Argument

Overview

Consider the following diagram offered by Craig:[9]

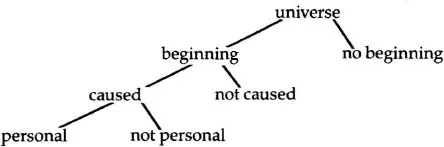
The kalam argument presents a number of dilemmas. First, the argument states that the universe either had a beginning or it did not. If it had a beginning, then this beginning was either caused or uncaused. If the beginning was caused, the cause was either personal or not personal. The burden of the argument is to establish one horn of each dilemma, and in so doing, to argue for the existence of a personal Creator. Thus, the argument attempts to show that there had to be a beginning to the universe which was caused by a personal Being.

In order to defend the argument, a premise must be established at each dilemma. Here are the major premises of the argument:

1. The universe had a beginning.
2. The beginning of the universe was caused.
3. The cause for the beginning of the universe was personal.

Set Theory

Before we attempt to establish these premises, it is important to distinguish between two kinds of infinity—a potential infinite and an actual infinite. The distinction goes back to Aristotle, but it has been made more precise in recent years by modern set theory.

Although some mathematicians distinguish between a class and a set, for our purposes it will suffice to use the two terms interchangeably. A set refers to a collection of objects called the members or elements of the set. For example, the set A, composed of my two children, Ashley and Allison, would be represented as follows:

A = {Ashley, Allison}

Similarly, the set B, composed of all the even integers from one to ten, would look like this:

B = {2, 4, 6, 8, 10}

Now we need to define the notion of a proper subset. A set C is a proper subset of a set D if and only if there is no member of C that is not a member of D, but there is a member of D that is not a member of C. Thus, the following set A1 is a proper subset of A:

A1 = {Ashley}

and B1 is a proper subset of B:

B1 = {2, 4}

If a set C is a proper subset of a set D, then C is a part of D or is contained in but not vice versa.

Before we can consider potential and actual infinites, one more set theoretic notion is important. This is the notion of the identity conditions for a set. Consider “two” sets, A and B, which are in fact the same set. Two sets, A and B, are identical if and only if each member of A is a member of B, and each member of B is a member of A. A set is defined by its membership. Two sets which have all and only the same members are really identical. There is an important implication from this fact. A set cannot change members by addition, subtraction, or any other way, and still be the same set. Once it adds or loses a member, it is no longer the same set. Sets and the properties which are true of them do not change. A set is considered timelessly and does not grow, decrease, or change through time.

Actual Infinity

We can now begin to consider the difference between an actual and a potential infinite by first studying some properties of infinite sets. According to Charles C. Pinter in Set Theory, “a finite set is one which ‘has n elements,’ where n is a natural number [one of the integers 1, 2, 3, . . .], and an infinite set is one which is not finite.”[10] A finite set has a definite number of elements which can be specified by counting the number of members in the set and assigning the appropriate number to that set. Thus, our set A had n = 2 elements, and B had n = 5.

An infinite set is very different from this. In order to see this, we need to define two notions: denumerability and one-to-one correspondence.[11] There is a one-to-one correspondence between two sets, A and B, if and only if the members of A can be paired with the members of B such that each member of A is paired with exactly one member of B and each member of B is paired with exactly one member of A. In other words, A and B have the same number of members. This is called having the same cardinal number.

Now assume one could form the set of all the natural numbers (e.g., 1, 2, 3, . . .). A set is denumerable if and only if it can be put in a one-to-one correspondence with the set of all the natural numbers. The set of all the natural numbers and all other denumerable sets (those with the same number of members as the set of natural numbers) is what we are calling an actual infinite. The set of natural numbers is usually given the name ω, and the cardinality of this set—the number of members in it—is called אa0 (aleph nought).

An actual infinite is a set considered as a completed totality with an actual infinite number of members. Among the most prominent of the definitions for an actual infinite set A are these two:

A is actually infinite if A has a denumerable subset.

A is actually infinite if A can be put into one-to-one correspondence with a proper subset of itself.

Consider two sets, E and F. E is the set of all the natural numbers. F is the set of all the even numbers. Which set has more members? You might be inclined to say that E has twice as many members as F. But according to infinite set theory, both sets have the same number of members, אa0. This can be seen by putting the two sets into one-to-one correspondence with one another:

E = 0 1 2 3 4 5 6 7 . . .
F = 0 2 4 6 8 10 12 14 . . .

F is a part of the whole, E. But since F and E are actual infinites, they are equal.

From the preceding discussion, several properties of actual infinites emerge. First, an actual infinite is a timeless totality which neither increases nor decreases in the number of members it contains. Second, a proper subset or part of an actual infinite can be put into one-to-one correspondence with (be made equal to) that actual infinite, as seen in E and F. This contrasts with a finite set, which cannot be put into one-to-one correspondence with one of its proper subsets. In finite sets, the whole is always greater than any of its proper parts.

Third, the following theorems could be proved of actually infinite sets: אa0 – 1 = אa0, אa0 + 1 = אa0, אa0 – n = אa0, אa0 + n = אa0, and (where n is any natural number), אa0 • אa0 = אa0. In addition, one can add or subtract denumerably many members from an actual infinite set and not change the number of members in the set! One interesting implication of these theorems has been stated by Geoffrey Hunter: “The number of points in infinite space of אa0 dimensions is the same as the number of points on a line a billionth of an inch.”[12]

Potential Infinity

In contrast to an actual infinite stands the notion of a potential infinite. The idea of a potential infinite is not a set theoretic idea at all, but occurs, among other places, in discussions about infinitesimal calculus. Perhaps you have seen this statement:

lim 1\n = 0
n → ∞

As mathematician Abraham Fraenkel puts it, this statement “asserts nothing about [actual] infini...

Table of contents

• Cover
• Title Page
• Copyright Page
• Dedication
• Table of Contents
• Foreword
• Acknowledgments
• Introduction
• 1. The Cosmological Argument
• 2. The Design Argument
• 3. God and the Argument from Mind
• 4. God and the Meaning of Life
• 5. The Historicity of the New Testament
• 6. The Resurrection of Jesus
• 7. Science and Christianity
• 8. Four Final Issues
• Conclusion
• Bibliography
• Index
• Notes
• Back Cover