Notes on the Synthesis of Form

Christopher Alexander

• Publisher: Harvard University Press
• Year: 1964
• Print ISBN: 9780674627505
• eBook ISBN: 9780674251915
• Topic: Architecture
• Subtopic: Architecture General

"These notes are about the process of design: the process of inventing things which display new physical order, organization, form, in response to function." This book, opening with these words, presents an entirely new theory of the process of design.

In the first part of the book, Christopher Alexander discusses the process by which a form is adapted to the context of human needs and demands that has called it into being. He shows that such an adaptive process will be successful only if it proceeds piecemeal instead of all at once. It is for this reason that forms from traditional un-self-conscious cultures, molded not by designers but by the slow pattern of changes within tradition, are so beautifully organized and adapted. When the designer, in our own self-conscious culture, is called on to create a form that is adapted to its context he is unsuccessful, because the preconceived categories out of which he builds his picture of the problem do not correspond to the inherent components of the problem, and therefore lead only to the arbitrariness, willfulness, and lack of understanding which plague the design of modern buildings and modern cities.

In the second part, Mr. Alexander presents a method by which the designer may bring his full creative imagination into play, and yet avoid the traps of irrelevant preconception. He shows that, whenever a problem is stated, it is possible to ignore existing concepts and to create new concepts, out of the structure of the problem itself, which do correspond correctly to what he calls the subsystems of the adaptive process. By treating each of these subsystems as a separate subproblem, the designer can translate the new concepts into form. The form, because of the process, will be well-adapted to its context, non-arbitrary, and correct.

The mathematics underlying this method, based mainly on set theory, is fully developed in a long appendix. Another appendix demonstrates the application of the method to the design of an Indian village.

1 / INTRODUCTION:
THE NEED FOR RATIONALITY

These notes are about the process of design; the process of inventing physical things which display new physical order, organization, form, in response to function.

Today functional problems are becoming less simple all the time. But designers rarely confess their inability to solve them. Instead, when a designer does not understand a problem clearly enough to find the order it really calls for, he falls back on some arbitrarily chosen formal order. The problem, because of its complexity, remains unsolved.

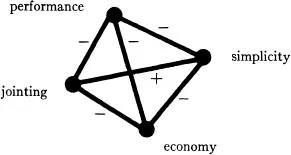
Consider a simple example of a design problem, the choice of the materials to be used in the mass production of any simple household object like a vacuum cleaner. Time and motion studies show that the fewer different kinds of materials there are, the more efficient factory assembly is — and therefore demand a certain simplicity in the variety of materials used. This need for simplicity conflicts with the fact that the form will function better if we choose the best material for each separate purpose separately. But then, on the other hand, functional diversity of materials makes for expensive and complicated joints between components, which is liable to make maintenance less easy. Further still, all three issues, simplicity, performance, and jointing, are at odds with our desire to minimize the cost of the materials. For if we choose the cheapest material for each separate task, we shall not necessarily have simplicity, nor optimum performance, nor materials which can be cleanly jointed. Writing a minus sign beside a line for conflict, and a plus beside a line for positive agreement, we see that even this simple problem has the five-way conflict pictured below.

This is a typical design problem; it has requirements which have to be met; and there are interactions between the requirements, which makes the requirements hard to meet. This problem is simple to solve. It falls easily within the compass of a single man’s intuition. But what about a more complicated problem?

Consider the task of designing a complete environment for a million people. The ecological balance of human and animal and plant life must be correctly adjusted both internally and to the given exterior physical conditions. People must be able to lead the individual lives they wish for. The social conditions induced must not lead to gross ill-health or to gross personal misery, and must not cause criminal delinquency. The cyclical intake of food and goods must not interfere with the regular movements of the inhabitants. The economic forces which develop must not lead to real-estate speculation which destroys the functional relation between residential areas and areas supporting heavy goods. The transportation system must not be organized so that it creates a demand that aggravates its own congestion. People must somehow be able to live in close cooperation and yet pursue the most enormous variety of interests. The physical layout must be compatible with foreseeable future regional developments. The conflict between population growth and diminishing water resources, energy resources, parklands, must somehow be taken care of. The environment must be organized so that its own regeneration and reconstruction does not constantly disrupt its performance.

As in the simpler example, each of these issues interacts with several of the others. But in this case each issue is itself a vast problem; and the pattern of interactions is vastly complicated. The difference between these two cases is really like the difference between the problem of adding two and two, and the problem of calculating the seventh root of a fifty digit number. In the first case we can quite easily do it in our heads. In the second case, the complexity of the problem will defeat us unless we find a simple way of writing it down, which lets us break it into smaller problems.

Today more and more design problems are reaching insoluble levels of complexity. This is true not only of moon bases, factories, and radio receivers, whose complexity is internal, but even of villages and teakettles. In spite of their superficial simplicity, even these problems have a background of needs and activities which is becoming too complex to grasp intuitively.

To match the growing complexity of problems, there is a growing body of information and specialist experience. This information is hard to handle; it is widespread, diffuse, unorganized.¹ Moreover, not only is the quantity of information itself by now beyond the reach of single designers, but the various specialists who retail it are narrow and unfamiliar with the form-makers’ peculiar problems, so that it is never clear quite how the designer should best consult them.² As a result, although ideally a form should reflect all the known facts relevant to its design, in-fact the average designer scans whatever information he happens on, consults a consultant now and then when faced by extra-special difficulties, and introduces this randomly selected information into forms otherwise dreamt up in the artist’s studio of his mind. The technical difficulties of grasping all the information needed for the construction of such a form are out of hand — and well beyond the fingers of a single individual.³

At the same time that the problems increase in quantity, complexity, and difficulty, they also change faster than before. New materials are developed all the time, social patterns alter quickly, the culture itself is changing faster than it has ever changed before. In the past — even after the intellectual upheaval of the Renaissance — the individual designer would stand to some extent upon the shoulders of his predecessors. And although he was expected to make more and more of his own decisions as traditions gradually dissolved, there was always still some body of tradition which made his decisions easier. Now the last shreds of tradition are being torn from him. Since cultural pressures change so fast, any slow development of form becomes impossible. Bewildered, the form-maker stands alone. He has to make clearly conceived forms without the possibility of trial and error over time. He has to be encouraged now to think his task through from the beginning, and to “create” the form he is concerned with, for what once took many generations of gradual development is now attempted by a single individual.⁴ But the burden of a thousand years falls heavily on one man’s shoulders, and this burden has not yet materially been lightened. The intuitive resolution of contemporary design problems simply lies beyond a single individual’s integrative grasp.

Of course there are no definite limits to this grasp (especially in view of the rare cases where an exceptional talent breaks all bounds). But if we look at the lack of organization and lack of clarity of the forms around us, it is plain that their design has often taxed their designer’s cognitive capacity well beyond the limit. The idea that the capacity of man’s invention is limited is not so surprising, after all. In other areas it has been shown, and we admit readily enough, that there are bounds to man’s cognitive and creative capacity. There are limits to the difficulty of a laboratory problem which he can solve;⁵ to the number of issues he can consider simultaneously;⁶ to the complexity of a decision he can handle wisely.⁷ There are no absolute limits in any of these cases (or usually even any scale on which such limits could be specified); yet in practice it is clear that there are limits of some sort. Similarly, the very frequent failure of individual designers to produce well organized forms suggests strongly that there are limits to the individual designer’s capacity.

We know that there are similar limits to an individual’s capacity for mental arithmetic. To solve a sticky arithmetical problem, we need a way of setting out the problem which makes it perspicuous. Ordinary arithmetic convention gives us such a way. Two minutes with a pencil on the back of an envelope lets us solve problems which we could not do in our heads if we tried for a hundred years. But at present we have no corresponding way of simplifying design problems for ourselves. These notes describe a way of representing design problems which does make them easier to solve. It is a way of reducing the gap between the designer’s small capacity and the great size of his task.

Part One contains a general account of the nature of design problems. It describes the way such problems have been solved in the past: first, in cultures where new problems are so rare that there are no actual designers; and then, by contrast, in cultures where new problems occur all the time, so that they have to be solved consciously by designers. From the contrast between the two, we shall learn how to represent a design problem so that it can be solved. Part Two describes the representation itself, and the kind of analysis the representation allows. Appendix 1 shows by example how the method works in practice.

The analysis of design problems is by no means obviously possible. There is a good deal of superstition among designers as to the deathly effect of analysis on their intuitions — with the unfortunate result that very few designers have tried to understand the process of design analytically. So that we get off to a fair start, let us try first to lay the ghosts which beset designers and make them believe that analysis is somehow at odds with the real problem of design.

It is not hard to see why the introduction of mathematics into design is likely to make designers nervous. Mathematics, in the popular view, deals with magnitude. Designers recognize, correctly, that calculations of magnitude only have strictly limited usefulness in the invention of form, and are therefore naturally rather skeptical about the possibility of basing design on mathematical methods.⁸ What they do not realize, however, is that modern mathematics deals at least as much with questions of order and relation as with questions of magnitude. And though even this kind of mathematics may be a poor tool if used to prescribe the physical nature of forms, it can become a very powerful tool indeed if it is used to explore the conceptual order and pattern which a problem presents to its designer.

Logic, like mathematics, is regarded by many designers with suspicion. Much of it is based on various superstitions about the kind of force logic has in telling us what to do. First of all, the word “logic” has some currency among designers as a reference to a particularly unpleasing and functionally unprofitable kind of formalism.⁹ The so-called logic of Jacques François Blondel or Vignola, for instance, referred to rules according to which the elements of architectural style could be combined.¹⁰ As rules they may be logical. But this gives them no special force unless there is also a legitimate relation between the system of logic and the needs and forces we accept in the real world. Again, the cold visual “logic” of the steel-skeleton office building seems horribly constrained, and if we take it seriously as an intimation of what logic is likely to do, it is certain to frighten us away from analytical methods.¹¹ But no one shape can any more be a consequence of the use of logic than any other, and it is nonsense to blame rigid physical form on the rigidity of logic. It is not possible to set up premises, trace through a series of deductions, and arrive at a form which is logically determined by the premises, unless the premises already have the seeds of a particular plastic emphasis built into them. There is no legitimate sense in which deductive logic can prescribe physical form for us.

But, in speaking of logic, we do not need to be concerned with processes of inference at all. While it is true that a great deal of what is generally understood to be logic is concerned with deduction, logic, in the widest sense, refers to something far more general. It is concerned with the form of abstract structures, and is involved the moment we make pictures of reality and then seek to manipulate these pictures so that we may look further into the reality itself. It is the business of logic to invent purely artificial structures of elements and relations. Sometimes one of these structures is close enough to a real situation to be allowed to represent it. And then, because the logic is so tightly drawn, we gain insight into the reality which was previously withheld from us.¹²

The use of logical structures to represent design problems has an important consequence. It brings with it the loss of innocence. A logical picture is easier to criticize than a vague picture since the assumptions it is based on are brought out into the open. Its increased precision gives us the chance to sharpen our conception of what the design process involves. But once what we do intuitively can be described and compared with nonintuitive ways of doing the same things, we cannot go on accepting the intuitive method innocently. Whether we decide to stand for or against pure intuition as a method, we must do so for reasons which can be discussed.

I wish to state my belief in this loss of innocence very clearly, because there are many designers who are apparently not willing to accept the loss. They insist that design must be a purely intuitive process: that it is hopeless to try and understand it sensibly because its problems are too deep.

There has already been one loss of innocence in the recent history of design; the discovery of machine tools to replace hand craftsmen. A century ago William Morris, the first man to see that the machines were being misused, also retreated from the loss of innocence. Instead of accepting the machine and trying to understand its implications for design, he went back to making exquisite handmade goods.¹³ It was not until Gropius started his Bauhaus that designers came to terms with the machine and the loss of innocence which it entailed.¹⁴

Now we are at a second watershed. This time the loss of innocence is intellectual rather than mechanical. But again there are people who are trying to pretend that it has not taken place. Enormous resistance to the idea of systematic processes of design is coming from people who recognize correctly the importance of intuition, but then make a fetish of it which excludes the possibility of asking reasonable questions.

It is perhaps worth remembering that the loss of intellectual innocence was put off once before. In the eighteenth century already, certain men, Carlo Lodoli and Francesco Algarotti in Italy and the Abbé Laugier in France, no longer content to accept the formalism of the academies, began to have serious doubts about what they were doing, and raised questions of just the sort that have led, a hundred and fifty years later, to the modern revolutionary ideas on form.¹⁵ Oddly enough, however, though these serious doubts were clearly expressed and widely read, architecture did not develop from them in the direction indicated. The doubts and questions were forgotten. Instead, in late eighteenth century Europe, we find evidence of quite another atmosphere developing, in which architects based their formal invention on the rules provide...

Table of contents

• Cover
• Title
• Copyright
• Contents
• 1. Introduction: The Need for Rationality
• Part One
• Part Two
• Appendices
• Notes