The Mathematics of Politics

E. Arthur Robinson, Daniel H. Ullman

• Publisher: CRC Press
• Year: 2016
• ISBN:
  9781498798907
• Topic: Matematica
• Subtopic: Matematica generale
• Edition: 2

It is because mathematics is often misunderstood, it is commonly

believed it has nothing to say about politics. The high school

experience with mathematics, for so many the lasting impression

of the subject, suggests that mathematics is the study of numbers,

operations, formulas, and manipulations of symbols. Those

believing this is the extent of mathematics might conclude

mathematics has no relevance to politics. This book counters this impression.

The second edition of this popular book focuses on mathematical reasoning

about politics. In the search for ideal ways to make certain kinds

of decisions, a lot of wasted effort can be averted if mathematics can determine that

finding such an ideal is actually impossible in the first place.

In the first three parts of this book, we address the following three

political questions:

(1) Is there a good way to choose winners of elections?

(2) Is there a good way to apportion congressional seats?

(3) Is there a good way to make decisions in situations of conflict and

uncertainty?

In the fourth and final part of this book, we examine the Electoral

College system that is used in the United States to select a president.

There we bring together ideas that are introduced in each of the three

earlier parts of the book.

Part III

Conflict

Introduction to Part III

If you believe in free will, then you believe that people are capable of making decisions. But how does a person make decisions? Sometimes, when presented with a decision problem, one can determine precisely what choices exist, ascertain what the outcome of every choice is, and evaluate these choices on a linear scale (by, for example, measuring the dollar value of each outcome). In such cases, decision-making is easy. One simply opts for the choice that maximizes benefit. But in the real world, decision-making is more difficult, because one faces uncertainty that may be of two types. The first type is uncertainty about nature. Nature may be thought of as random and unconcerned with our welfare. For example, to decide whether to carry an umbrella, we should factor in the probability of rain. The second type is uncertainty about people. A person, unlike nature, may be our friend or our adversary, and a person may have a stake in the decision process that is unrelated to ours. We assume that other people do not act randomly but rather act in their own self-interest. In other words, they act like we do. For example, to decide how to negotiate a treaty, we need to contemplate the point of view of other signatories.

In Part III, we introduce a context for making decisions in the face of uncertainty. To provide some structure for our model, we assume that the decision-makers know what choices are available to them and to the other decision-makers, and we assume that the outcomes of these decisions can be objectively evaluated on a linear scale. These things are regarded as certain. The uncertainty stems either from random nature or from savvy opponents.

We manage uncertainty about nature with probability theory. We manage uncertainty about people with game theory. In the context of the phrase “game theory”, a game need not be entertaining like Monopoly or frivolous like tic-tac-toe. A game is simply a framework for modeling the decision-making process. In our games, several players — usually just two — simultaneously render a decision. The possible choices for all players are known to all players, and the values of all outcomes — often thought of in terms of dollar values — are also known to all. Once the decisions are revealed, the outcome of the game is completely determined, the players are paid their due, and the game ends. We discover that probability theory is an important paradigm for analyzing games, even when there does not seem to be any randomness involved in the rules of the game itself.

Uncertainty generally makes people uncomfortable. It is rare for politicians to admit to uncertainty, and yet uncertainty is present in all complex policy decisions. By contrast, weather forecasters are more frank about their uncertainty, admitting on a daily basis the degree of their uncertainty about the subsequent day’s likelihood of rain. Yet an indifferent natural world and cunning adversaries lurk everywhere in the political realm, and therefore a rational analysis of decisions requires both probabilistic and game-theoretic reasoning. It would be refreshing to hear politicians more often admit to employing the type of rational analysis that we encounter here in Part III.

13

Strategies and Outcomes

“The score never interested me, only the game.” — Mae West

13.0 Scenario

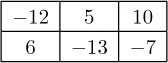
Let’s play a game. We begin with a matrix of numbers, like this:

Game 13.1 A simple matrix game.

There are two players in this game, and we call them “Row” and “Column”. Both players know all of the entries in the matrix. To play the game, Row secretly chooses a row (there are two choices available to her), and Column secretly — and independently — chooses a column (there are three choices available to him). Then the two players simultaneously reveal their choices. This identifies one particular entry in the matrix. For example, if Row chooses row 2 and Column chooses column 1, the entry “6” in the lower left entry is identified. This entry represents the number of dollars that Column must pay to Row: On the other hand, if the entry were negative, like the −12 in the upper left, then Row would have to pay Column. If Row selects her first row and Column selects his first column, then Row must pay Column $12.

How should the two players make their decisions? For each player, which choice is the safest? Which choice is the boldest? Remember that the information in the matrix is public, so it is possible for the two players to put themselves in the shoes of their opponents. Both players are clever and want to win as much money as possible. But they each recognize that their opponent is like-minded.

13.1 Zero-Sum Games

In this chapter we introduce a type of game called a two-person zero-sum game. We start by looking at a familiar example: a children’s game called Roshambo. Lest the reader feel that game theory is not serious, however, we also consider a game that models a naval battle from World War II.

The game of Roshambo, known more familiarly in the United States as Rock-Paper-Scissors, is played by children throughout the world. Recently, Roshambo has also become a popular tournament game in bars. To play Roshambo, two players face each other, and, on the count of three, each makes a finger gesture representing Rock, Paper, or Scissors. The gesture for Rock is a closed fist, the gesture for Paper is an open palm, and the gesture for Scissors is two fingers. Certain gestures defeat others: Rock beats Scissors (i.e., rock dulls scissors), Scissors beats Paper (scissors cut paper), and Paper beats Rock (paper covers rock). If both players make the same gesture, then the outcome is considered to be a tie.

The choices available to a player in a game are called the player’s strategies. We generally call the two players Row and Column. For the purpose of choosing appropriate pronouns, we often imagine that Row is female and Column is male. In Roshambo, each player has three strategies from which to choose: Rock, Paper, and Scissors. A single round of play involves the players choosing strategies, and then, at a prescribed moment, simultaneously revealing their strategy choices. A strategy choice by each player determines an outcome of the game. For example, in Roshambo, if Row chooses Rock and Column chooses Paper, then the outcome is (Rock, Paper). Since Paper beat...