Statistical Rethinking

A Bayesian Course with Examples in R and STAN

Richard McElreath

• Publisher: Chapman and Hall/CRC
• Year: 2020
• ISBN:
  9780429639142
• Edition: 2
• Topic: Mathematics
• Subtopic: Mathematics General
• Index: Mathematics

Statistical Rethinking: A Bayesian Course with Examples in R and Stan builds your knowledge of and confidence in making inferences from data. Reflecting the need for scripting in today's model-based statistics, the book pushes you to perform step-by-step calculations that are usually automated. This unique computational approach ensures that you understand enough of the details to make reasonable choices and interpretations in your own modeling work.

The text presents causal inference and generalized linear multilevel models from a simple Bayesian perspective that builds on information theory and maximum entropy. The core material ranges from the basics of regression to advanced multilevel models. It also presents measurement error, missing data, and Gaussian process models for spatial and phylogenetic confounding.

The second edition emphasizes the directed acyclic graph (DAG) approach to causal inference, integrating DAGs into many examples. The new edition also contains new material on the design of prior distributions, splines, ordered categorical predictors, social relations models, cross-validation, importance sampling, instrumental variables, and Hamiltonian Monte Carlo. It ends with an entirely new chapter that goes beyond generalized linear modeling, showing how domain-specific scientific models can be built into statistical analyses.

Features

• 
  
  

• Integrates working code into the main text

• 
  
  

• Illustrates concepts through worked data analysis examples

• 
  
  

• Emphasizes understanding assumptions and how assumptions are reflected in code

• 
  
  

• Offers more detailed explanations of the mathematics in optional sections

• 
  
  

• Presents examples of using the dagitty R package to analyze causal graphs

• 
  
  

• Provides the rethinking R package on the author's website and on GitHub

1 The Golem of Prague

In the sixteenth century, the House of Habsburg controlled much of Central Europe, the Netherlands, and Spain, as well as Spain’s colonies in the Americas. The House was maybe the first true world power. The Sun shone always on some portion of it. Its ruler was also Holy Roman Emperor, and his seat of power was Prague. The Emperor in the late sixteenth century, Rudolph II, loved intellectual life. He invested in the arts, the sciences (including astrology and alchemy), and mathematics, making Prague into a world center of learning and scholarship. It is appropriate then that in this learned atmosphere arose an early robot, the Golem of Prague.

A golem (goh-lem) is a clay robot from Jewish folklore, constructed from dust and fire and water. It is brought to life by inscribing emet, Hebrew for “truth,” on its brow. Animated by truth, but lacking free will, a golem always does exactly what it is told. This is lucky, because the golem is incredibly powerful, able to withstand and accomplish more than its creators could. However, its obedience also brings danger, as careless instructions or unexpected events can turn a golem against its makers. Its abundance of power is matched by its lack of wisdom.

In some versions of the golem legend, Rabbi Judah Loew ben Bezalel sought a way to defend the Jews of Prague. As in many parts of sixteenth century Central Europe, the Jews of Prague were persecuted. Using secret techniques from the Kabbalah, Rabbi Judah was able to build a golem, animate it with “truth,” and order it to defend the Jewish people of Prague. Not everyone agreed with Judah’s action, fearing unintended consequences of toying with the power of life. Ultimately Judah was forced to destroy the golem, as its combination of extraordinary power with clumsiness eventually led to innocent deaths. Wiping away one letter from the inscription emet to spell instead met, “death,” Rabbi Judah decommissioned the robot.

1.1. Statistical golems

Scientists also make golems.¹ Our golems rarely have physical form, but they too are often made of clay, living in silicon as computer code. These golems are scientific models. But these golems have real effects on the world, through the predictions they make and the intuitions they challenge or inspire. A concern with “truth” enlivens these models, but just like a golem or a modern robot, scientific models are neither true nor false, neither prophets nor charlatans. Rather they are constructs engineered for some purpose. These constructs are incredibly powerful, dutifully conducting their programmed calculations.

Sometimes their unyielding logic reveals implications previously hidden to their designers. These implications can be priceless discoveries. Or they may produce silly and dangerous behavior. Rather than idealized angels of reason, scientific models are powerful clay robots without intent of their own, bumbling along according to the myopic instructions they embody. Like with Rabbi Judah’s golem, the golems of science are wisely regarded with both awe and apprehension. We absolutely have to use them, but doing so always entails some risk.

There are many kinds of statistical models. Whenever someone deploys even a simple statistical procedure, like a classical t-test, she is deploying a small golem that will obediently carry out an exact calculation, performing it the same way (nearly²) every time, without complaint. Nearly every branch of science relies upon the senses of statistical golems. In many cases, it is no longer possible to even measure phenomena of interest, without making use of a model. To measure the strength of natural selection or the speed of a neutrino or the number of species in the Amazon, we must use models. The golem is a prosthesis, doing the measuring for us, performing impressive calculations, finding patterns where none are obvious.

However, there is no wisdom in the golem. It doesn’t discern when the context is inappropriate for its answers. It just knows its own procedure, nothing else. It just does as it’s told. And so it remains a triumph of statistical science that there are now so many diverse golems, each useful in a particular context. Viewed this way, statistics is neither mathematics nor a science, but rather a branch of engineering. And like engineering, a common set of design principles and constraints produces a great diversity of specialized applications.

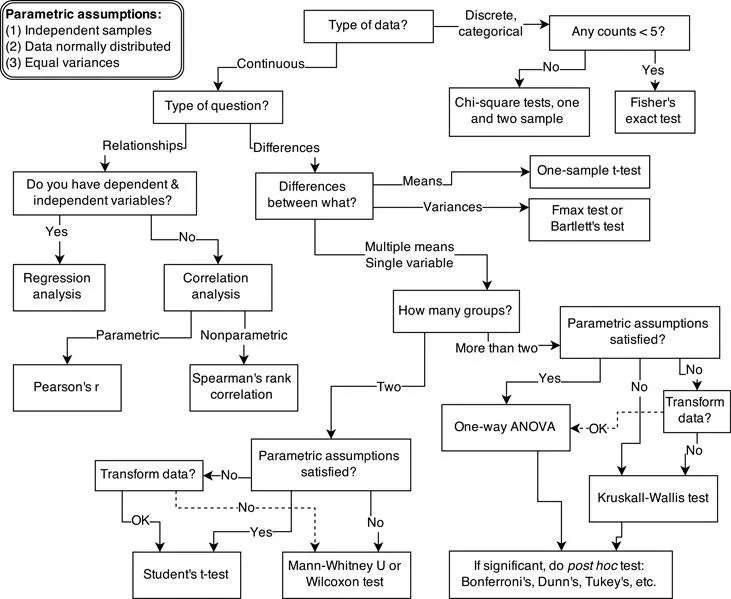
This diversity of applications helps to explain why introductory statistics courses are so often confusing to the initiates. Instead of a single method for building, refining, and critiquing statistical models, students are offered a zoo of pre-constructed golems known as “tests.” Each test has a particular purpose. Decision trees, like the one in FIGURE 1.1, are common. By answering a series of sequential questions, users choose the “correct” procedure for their research circumstances.

FIGURE 1.1. Example decision tree, or flowchart, for selecting an appropriate statistical procedure. Beginning at the top, the user answers a series of questions about measurement and intent, arriving eventually at the name of a procedure. Many such decision trees are possible.

Unfortunately, while experienced statisticians grasp the unity of these procedures, students and researchers rarely do. Advanced courses in statistics do emphasize engineering principles, but most scientists never get that far. Teaching statistics this way is somewhat like teaching engineering backwards, starting with bridge building and ending with basic physics. So students and many scientists tend to use charts like FIGURE 1.1 without much thought to their underlying structure, without much awareness of the models that each procedure embodies, and without any framework to help them make the inevitable compromises required by real research. It’s not their fault.

For some, the toolbox of pre-manufactured golems is all they will ever need. Provided they stay within well-tested contexts, using only a few different procedures in appropriate tasks, a lot of good science can be completed. This is similar to how plumbers can do a lot of useful work without knowing much about fluid dynamics. Serious trouble begins when scholars move on to conducting innovative research, pushing the boundaries of their specialties. It’s as if we got our hydraulic engineers by promoting plumbers.

Why aren’t the tests enough for research? The classical procedures of introductory statistics tend to be inflexible and fragile. By inflexible, I mean that they have very limited ways to adapt to unique research contexts. By fragile, I mean that they fail in unpredictable ways when applied to new contexts. This matters, because at the boundaries of most sciences, it is hardly ever clear which procedure is appropriate. None of the traditional golems has been evaluated in novel research settings, and so it can be hard to choose one and then to understand how it behaves. A good example is Fisher’s exact test, which applies (exactly) to an extremely narrow empirical context, but is regularly used whenever cell counts are small. I have personally read hundreds of uses of Fisher’s exact test in scientific journals, but aside from Fisher’s original use of it, I have never seen it used appropriately. Even a procedure like ordinary linear regression, which is quite flexible in many ways, being able to encode a large diversity of interesting hypotheses, is sometimes fragile. For example, if there is substantial measurement error on prediction variables, then the procedure can fail in spectacular ways. But more importantly, it is nearly always possible to do better than ordinary linear regression, largely because of a phenomenon known as OVERFITTING (Chapter 7).

The point isn’t that statistical tools are specialized. Of course they are. The point is that classical tools are not diverse enough to handle many common research questions. Every active area of science contends with unique difficulties of measurement and interpretation, converses with idiosyncratic theories in a dialect barely understood by other scientists from other tribes. Statistical experts outside the discipline can help, but they are limited by lack of fluency in the empirical and theoretical concerns of the discipline.

Furthermore, no statistical tool does anything on its own to address the basic problem of inferring causes from evidence. Statistical golems do not understand cause and effect. They only understand association. Without our guidance and skepticism, pre-manufactured golems may do nothing useful at all. Worse, they might wreck Prague.

What researchers need is some unified theory of golem engineering, a set of principles for designing, building, and refining special-purpose statistical procedures. Every major branch of statistical philosophy possesses such a unified theory. But the theory is never taught in introductory—and often not even in advanced—courses. So there are benefits in rethinking statistical inference as a set of strategies, instead of a set of pre-made tools.

1.2. Statistical rethinking

A lot can go wrong with statistical inference, and this is one reason that beginners are so anxious about it. When the goal is to choose a pre-made test from a flowchart, then the anxiety can mount as one worries about choosing the “correct” test. Statisticians, for their part, can derive pleasure from scolding scientists, making the psychological battle worse.

But anxiety can be cultivated into wisdom. That is the reason that this book insists on working with the computational nuts and bolts of each golem. If you don’t understand how the golem processes information, then you can’t interpret the golem’s output. This requires knowing the model in greater detail than is customary, and it requires doing the computations the hard way, at least until you are wise enough to use the push-button solutions.

There are conceptual obstacles as well, obstacles with how scholars define statistical objectives and interpret statistical results. Understanding any individual golem is not enough, in these cases. Instead, we need some statistical epistemology, an appreciation of how statistical models relate to hypotheses and the natural mechanisms of interest. What are we supposed to be doing with these little computational machines, anyway?

The greatest obstacle that I encounter among students and colleagues is the tacit belief that the proper objective of statistical inference is to test null hypotheses.³ This is the proper objective, the thinking goes, because Karl Popper argued that science advances by falsifying hypotheses. Karl Popper (1902–1994) is possibly the most influential philosopher of science, at least among scientists. He did persuasively argue that science works better by developing hypotheses that are, in principle, falsifiable. Seeking out evidence that might embarrass our ideas is a normative standard, and one that most scholars—whether they describe themselves as scientists or not—subscribe to. So maybe statistical procedures should falsify hypotheses, if we wish to be good statistical scientists.

But the above is a kind of folk Popperism, an informal philosophy of science common among scientists but not among philosophers of science. Science is not described by the falsification standard, and Popper recognized that.⁴ In fact, deductive falsification is impossible in nearly every scientific context. In this section, I review two reasons for this impossibility.

(1) Hypotheses are not models. The relations among hypotheses and different kinds of models are complex. Many models correspond to the same hypothesis, and many hypotheses correspond to a single model. This makes strict falsification impossible.

(2) Measurement matters. Even when we think the data falsify a model, another observer will debate our methods and measures. They don’t trust the data. Sometimes they are right.

For both of these reasons, deductive falsification never works. The scientific method cannot be reduced to a statistical procedure, and so our statistical methods should not pretend. Statistical evidence is part of the hot mess that is science, with all of its combat and egotism and mutual coercion. If you believe, as I do, that science does often work, then learning that it doesn’t work via falsification shouldn’t change your mind. But it might help you do better science. It might open your eyes to many legitimately useful functions of statistical golems.

Rethinking: Is NHST falsificationist? Null hypothesis significance testing, NHST, is often identified with the falsificationist, or Popperian, philosophy of science. However, usually NHST is used to falsify a null hypothesis, not the actual research hypothesis. So the falsification is being done to something other than the explanatory model. This seems the reverse from Karl Popper’s philosophy.⁵

1.2.1. Hypotheses are not models. When we attempt to falsify a hypothesis, we must work with a model of some kind. Even when the attempt is not explicitly statistical, there is always a tacit model of measurement, of evidence, that operationalizes the hypothesis. All models are false,⁶ so what does it mean to falsify a model? One consequence of the requirement to work with models is that it’s no longer possible to deduce that a hypothesis is false, just because we reject a model derived from it.

Let’s explore this consequence in the context of an example from population biology (FIGURE 1.2). Beginning in the 1960s, evolutionary biologists became interested in the proposal that the majority of evolutionary changes i...