Weirdest Maths

At the Frontiers of Reason

David Darling, Agnijo Banerjee

• Publisher: Oneworld Publications
• Year: 2021
• eBook ISBN: 9781786078063
• Topic: Mathematics
• Subtopic: History & Philosophy of Mathematics
• Index: Mathematics

Maths is everywhere, in everything. It’s in the finest margins of modern sport. It’s in the electrical pulses of our hearts and the flight of every bird. It is our key to secret messages, lost languages and perhaps even the shape of the universe of itself.

David Darling and Agnijo Banerjee reveal the mathematics at the farthest reaches of our world – from its role in the plots of novels to how animals employ numerical skills to survive. Along the way they explore what makes a genius, why a seemingly simple problem can confound the best and brightest for decades, and what might be the great discovery of the twenty-first century. As Bertrand Russell once said, ‘mathematics, rightly viewed, possesses not only truth, but supreme beauty’. Banerjee and Darling make sure we see it right again.

‌Chapter 1

Genius

Talent is a flame. Genius is a fire.

– Bernard Williams

When he was six, John von Neumann could multiply and divide two 8-digit numbers in his head. A couple of years later he’d progressed to solving tough problems in differential and integral calculus. He’d also amuse his parents’ friends by chatting in ancient Greek or reciting whole pages of a telephone directory that he’d memorised at a glance – early signs of the startling ability that would blossom in adulthood. Economist Paul Samuelson said of von Neumann that he had ‘the fastest mind’ of anyone he’d met. Polish-born British mathematician Jacob Bronowski, in the 1973 documentary series The Ascent of Man, considered him ‘the cleverest man I ever knew, without exception’ (the second cleverest he judged to be Italian-American physicist Enrico Fermi).

These days ‘genius’ is a much overused label. It’s also, like beauty, an imprecise one that’s partly in the eye of the beholder. The claim to be able to measure the threshold of genius with a single number – an ‘intelligence quotient’ or IQ – just doesn’t bear scrutiny. A commonly applied type of IQ test, based on the work of French psychologist Alfred Binet in the early twentieth century, puts a figure of 100 or thereabouts on average intelligence and rates genius as anything above about 160. But like the cryptic crossword puzzles in a newspaper, IQ tests are things you get better at with practice and age (up to a point). They also favour certain types of thinker. Who’d feel happy about ranking the relative genius of Beethoven, Picasso, and Einstein based, say, on their scores in the entrance test to Mensa? Richard Feynman, by common consent one of the brightest theoretical physicists of the twentieth century, and co-winner of the 1965 Nobel Prize for Physics (with Julian Schwinger and Sin-Itiro Tomonaga), managed just 125 in a high school IQ test. My co-author, Agnijo, took the Mensa entrance test at age twelve and achieved a maximum possible score of 162, putting him ahead of Stephen Hawking at the same age. But he’s modest enough to recognise that such comparisons are meaningless unless a great intellect is turned to good use later in life.

What is genius – and, in particular, mathematical genius? Does the potential for it lie within each of us if only we knew how to tap it? Or does the spark of genius have to be there from the start, in the makeup of an individual’s brain? There are no easy answers because the forms in which exceptional ability and achievements come are so varied.

John von Neumann, for instance, though unquestionably a genius by any definition, had a privileged upbringing. Born to Jewish parents in Budapest in 1903, he was given every advantage money could buy including, at the age of eight, entrance to the Fasori Evangélikus Gimnázium, one of three prep schools at the pinnacle of a superb education system in the Hungarian capital – for those who could afford it. Between the late 1890s and the 1930s, this elite system turned out a generation of mega-intellects who played important roles on the world stage of science and maths: von Neumann himself, mathematician and space engineer Theodore von Kármán, radiochemist George de Hevesy, physicists Leó Szilárd, Eugene Wigner, and Edward Teller, and extraordinarily prolific mathematician Paul Erdős, among them. Most of these talented Jewish Hungarians ended up in the United States in the first half of the twentieth century and soon gained a reputation for their almost superhuman abilities. On one occasion, Szilárd was asked why no intelligent extraterrestrials had been found despite the seeming likelihood that they existed – the so-called Fermi Paradox. He replied: ‘They are already here among us – they just call themselves Hungarians.’

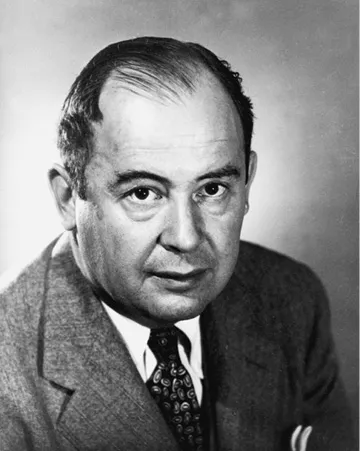
John von Neumann, widely regarded as one of the greatest mathematical geniuses of the twentieth century, shown here in 1956.

No one would claim that eastern Europeans are inherently smarter than anyone else. All the Hungarian example shows is that the right upbringing and education can help foster intellectual attainment, but there’s surely more to genius than that. Some of the greatest mathematicians the world has ever known came from humble backgrounds.

Take Carl Friedrich Gauss, born in 1777 in what’s now Lower Saxony, Germany. Today, he stands shoulder to shoulder with the likes of Euclid, Isaac Newton, and Leonhard Euler as a colossus of mathematics. Yet his origins were humble. His father turned his hand to gardening, bricklaying, butchering, and anything else that would help make ends meet. His mother could neither read nor write and never recorded the date of Carl’s birth. She did remember, though, that it was on a Wednesday, eight days before the Feast of Ascension, which, in turn, is the fortieth day of Easter. In time, Gauss came up with a formula that gave not only his own birthdate but also the date of Easter in any year, past or future.

Even as a toddler, Carl’s talent with numbers stood out: he could do sums when he could barely speak. Just after he’d turned three, he spotted a mistake in his father’s tax calculations. As a seven-year-old, he solved a problem in seconds that his teacher had expected would keep his class busy for ages. The problem was to add together all the numbers from one to a hundred. Gauss quickly spotted that the sum could be broken down into fifty pairs – (1 + 100) + (2 + 99) + … + (50 + 51) – each of which added up to 101, giving a total of 101 times 50, or 5050. By the age of ten he’d discovered an important result in maths called the binomial theorem that, unbeknown to him, had been derived earlier by Newton. Word spread of the young prodigy’s achievements and he found a sponsor in the Duke of Brunswick who offered to fund his further education.

Thanks to his benefactor, Gauss was able to attend the Collegium Carolinum – where he earned a degree in maths at the age of eighteen – and then move on to the prestigious University of Göttingen for his graduate studies. In 1796, a year after receiving his doctorate, he cracked a major problem in geometry by showing that a regular polygon with 17 sides could be constructed using just an unmarked ruler and a compass. The Greeks had known how to construct polygons with 3, 5, and 15 sides with ruler and compass alone but making the heptadecagon in the same way had resisted all their efforts. It was this breakthrough that persuaded Gauss to focus on maths instead of languages, at which he also excelled. Later in the same year, he discovered that every number is the sum of at most three triangular numbers (numbers of the form 1 + 2 + … + n, for example 1, 3, 6, or 5050).

One of Gauss’s most spectacular achievements was to track down a heavenly body that had gone missing. In 1801, Italian astronomer Giuseppe Piazzi discovered a faint object, which he called Ceres, that didn’t appear in catalogues of known stars at the time. Piazzi followed Ceres over a period of several weeks and found that it wasn’t a star at all but something in orbit around the Sun. Then he fell ill and lost track of the newcomer. Fortunately, Gauss was able to figure out its orbit, along with its whereabouts, using just the handful of observations that Piazzi had already made. As we now know, Ceres is the largest object in the asteroid belt, so large, in fact, that it’s been reclassified as a dwarf planet.

Gauss showed an exceptional talent for maths even before he started school. His genius, it seems, was innate – although who knows if it would have flourished later on had not his ability been recognised and allowed to develop. In some ways his story parallels that of another genius who lived more recently.

The most extraordinary mathematician of the twentieth century was born, like Gauss, to working-class parents and had, early on, a very modest education. Yet by the age of eleven, when he encountered formal maths in school for the first time, it was already clear that Srinivasa Ramanujan was operating on a different plane. In his early teens he tutored other pupils, mastered new concepts with ease, and won a string of academic awards. In 1903, as a sixteen-year-old, he got hold of a library copy of a book with the disarmingly simple title A Synopsis of Elementary Results, which, in fact, was a dense collection of about five thousand results in pure maths based on the notoriously challenging Mathematical Tripos at Cambridge. Not satisfied merely to absorb the book’s contents, Ramanujan set out to derive all of its results himself with no outside help. In the process he came up with a wealth of other extraordinary conclusions that seemed to spring from nowhere.

This almost manic creativity, with no obvious point of origin, became a hallmark of Ramanujan’s work. To the end of his life, he attributed all of his major insights and discoveries to a singular source beyond logic – the Goddess of Namagiri (his hometown) who, he said, appeared to him in visions and revealed formulae, which, upon waking, he’d seek to verify. Ramanujan’s proofs, however, were often incomplete, making it hard to check them or sometimes even to make sense of his propositions. They were also, sometimes, just plain wrong.

It’s possible that Ramanujan would have remained in relative obscurity had he not, in his twenties, written a series of letters to distinguished British mathematicians. Only one of them took him seriously. Fortunately, that one happened to be G. H. Hardy, famed Cambridge scholar and distinguished number theorist who had himself been precocious as a child. While still a toddler he wrote down numbers into the millions and, later, when taken to church on the Sabbath he’d pass the time factorising the numbers of hymns. In Ramanujan’s writings, Hardy recognised something very special indeed. Some of the Indian’s results corresponded to known maths, but of a very advanced nature and arrived at by unfamiliar means. Other results seemed utterly new but, in Hardy’s opinion, probably true ‘because, if they were not true, no one would have the imagination to invent them’. In Ramanujan’s obituary, which, sadly, Hardy would pen just seven years later, he wrote that Ramanujan was ‘a mathematician of the highest quality, a man of altogether exceptional originality and power’. On his personal scale of maths ability, Hardy scored himself a modest 25, another close colleague at Cambridge, John Littlewood, 30, and David Hilbert, the most renowned mathematician of the time, 80. Ramanujan he rated at 100.

Hardy invited Ramanujan to join him at Cambridge and for a few years the two formed a formidable team, at the very college, Trinity, where Agnijo now studies. Hardy taught the younger man how to set down proofs in an orthodox way so that they could be published in academic journals and checked by other mathematicians. At the same time, he was aware that it was neither possible nor desirable to give the Indian a conventional education in all the areas of maths that he’d missed. Hardy understood well the danger of such an education: that it can stifle the kind of extreme creativity that’s so often the sign and greatest product of true genius.

Knowing too much about a subject can make us overly cautious. Having a lot of conventional wisdom may make us doubt our own hunches and intuition because we’re more likely to think that any seemingly good ideas that pop into our heads are wrong if they don’t square with what we’ve previously learned. Had Ramanujan received an expensive but traditional education, would his genius have burned so brightly and uniquely? For sure, mathematical genius needs some foundation on which to build, but what’s the optimal amount of formal schooling to nurture genius but not at the same time crush it with conformity?

The strangest aspect of Ramanujan’s genius was his conviction that it had a supernatural source. Artists and musicians have often, especially in the past, expressed the view that their work was divinely inspired. Kahlil Gibran, the Lebanese-American mystic poet and artist, wondered: ‘Am I a harp that the hand of the almighty may touch me or a flute that his breath may pass through me?’ It’s more unusual for mathematicians or scientists to regard themselves as agents of a higher power, but it’s common for them to talk about the importance of sudden inspiration. Famously, the German chemist August Kekulé ascribed his discovery of the benzene ring to a dream in which he saw a serpent with a tail in its mouth – an ancient symbol, known as the ouroboros (Greek for ‘tail-devourer’), representing an endless cycle or loop. French philosopher and mathematician René Descartes and mathematician Henri Poincaré also accounted for some of their importan...

Table of contents

• About the Authors
• Introduction
• Chapter 1 • Genius
• Chapter 2 • Sporting Chance
• Chapter 3 • For Your Eyes Only
• Chapter 4 • Fantasia Mathematica
• Chapter 5 • In Beauty Lies Truth?
• Chapter 6 • The Shape of Space
• Chapter 7 • Life by Numbers
• Chapter 8 • Stats Weird
• Chapter 9 • Easier Said Than Done
• Chapter 10 • Anything You Can Do…
• Chapter 11 • Logic: Formal, Fallacious, and Fuzzy
• Chapter 12 • Is Everything Mathematical?
• Chapter 13 • The Next Fifty Years
• Acknowledgements