The Learning and Teaching of Number

Paths Less Travelled Through Well-Trodden Terrain

Rina Zazkis, John Mason, Igor' Kontorovich

• Publisher: Routledge
• Year: 2021
• eBook ISBN: 9780429757952
• Topic: Education
• Subtopic: Education General

Numbers are the backbones of mathematics. From 1 to infinity, numbers accompany and underlie the learning of mathematics and research. While perceived as familiar and understood, numbers present fascinating and often mysterious patterns, relationships and pedagogical issues. The Learning and Teaching of Number explores how mathematics education research has addressed issues related to the structure of numbers and number operations and provides a classroom context. It invites readers to explore less-travelled paths through a well-trodden terrain of number.

This fascinating book combines mathematical content with pedagogical ideas and research results. Focusing on number, the book illustrates central ideas related to numbers via a variety of tasks at different levels of complexity. The Learning and Teaching of Number will allow the reader to

• examine and develop personal understanding of number sets and the relationships among them;
• enhance personal understanding of familiar topics associated with number operations;
• engage in a variety of tasks and strengthen personal problem-solving skills;
• enrich their repertoire of mathematical tasks and pedagogical actions; and
• consider research ideas and results related to teaching numbers, number operations and number relationships.

This is a valuable resource for teacher education courses, graduate programs in mathematics education and professional development programs. Teacher trainers and maths teachers will find their personal understanding of numbers and relationships enriched and will draw connections between research and classroom pedagogy which will extend and enhance their teaching.

Snapshot 1
CAPTURING NUMBERS

Numbers have verbal names and symbolic representations.¹ Strictly speaking, the symbols 1, 2, 3, 4, … are numerals. They are not themselves numbers, but names or symbols serving to denote or refer to numbers. These well-accepted and succinct symbols feature one of several common representations to capture numbers. In ancient times, numbers were represented by tallies, such as markings on a stick or pebbles in a bowl. However, as numbers got bigger, the development of some more succinct notation became essential. In this snapshot we review several ways to capture numbers through different representations. Note that each representation stresses some number features and ignores others.

1 Denoting

Write down a number that describes how many ducks there are in Figure 1.1. For the same ducks, make another, different record; and another; …; and another.

FIGURE 1.1 Some number of ducks

Most people write or at least imagine “5”. People with English as their first language can say “five”. The names “5” and “five” are the most readily accessed elements in their example space. Closely connected are decompositions such as 1 + 4, or 1 + 2 + 2. Tasks like this can be carried out in kindergarten, where children can be asked to make a record so that they can look at their record and know without looking at them how many ducks there are (Hughes, 1986). But such tasks can also be worthwhile for prospective teachers and others, since they can potentially lead to engaging discussions on number representation.

Indeed, “5” is the obvious choice for representing the number of ducks in the picture. However, is there another way to capture this number?

The strategy of asking for “another, and another” was developed by Watson and Mason (2005) in their work on learner generated examples. They described this strategy as a valuable pedagogy which pushes the learner to consider examples beyond those immediately available and so to extend personal example spaces. The size, diversity and richness of interconnections of personal example spaces indicate the quality of understanding.

Describing the number of ducks in Figure 1.1, we write “5”, or “five” or “cinco”. From there, this seemingly naïve task can be developed in different directions. One possible direction, which usually comes up in a class of (prospective) teachers, is acknowledgement of other ways to write down “five”, such as V or

. The symbol “V” is a familiar Roman numeral, so we direct readers’ attention to the symbol “

” and Figure 1.2.

FIGURE 1.2 Arabic digits

Figure 1.3 shows the banknote of five pounds used in Egypt, of five riyals used in Saudi Arabia and of five dinars used in Jordan. The symbol “

” can be clearly identified, while the opposite sides of the bills denote the value as “5” and “five”.

FIGURE 1.3 Banknotes used in Egypt, Saudi Arabia and Jordan

It is often a surprise that while today the commonly used digit symbols and numeration system are referred to as Arabic or Hindu-Arabic (also Indo-Arabic, e.g., Ore, 1998), different symbols for digits are used in some Arab countries. But this surprise is an opportunity to focus on the distinction between symbols for digits and a numeration system. While V and

both represent the number that English speakers call “five”, the difference between symbols and numeration systems is highlighted when we represent, for example, “thirty-seven” with symbols.

Compare: 37

XXXVII

Note the number of symbols and the correspondence among the different symbols in the three representations. And how about larger numbers, like four thousand seventy-six?

TASK: EXPERIENCING THE DIFFERENCE BETWEEN NUMBER REPRESENTATIONS

Represent the numbers “four thousand seventy-six” and “five thousand five hundred and seven” with (a) Roman numerals and (b) digit symbols from Figure 1.2.

Discuss what each numeral system highlights or stresses and what it puts in the background or ignores.

Such a task emphasizes that the strangely written symbols in Figure 1.2 are part of the same conventional numeration system that we use and are used to, while the more familiar Roman numerals are part of a very different numeration system. To recall, the main components of Hindu-Arabic numeration system are positional notation, also known as place value; base-ten; and ten symbols for digits conventionally denoted with “1”, “2”, “3”, “4”, “5”, “6”, “7”, “8”, “9” and “0”. Thus, the symbol sequence 10 is made up of two symbols and actually means “one ten and no units”. “Ten” itself has no self-contained symbol.

Returning to the number “five”, we have noted an example, namely Roman numerals, that does not use our standard positional notation. We have also seen an example of different symbols used for...

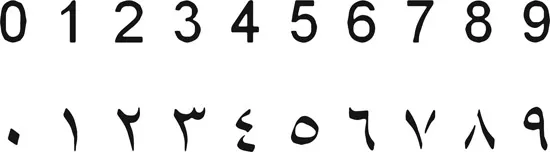
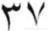
Table of contents

• Cover
• Half Title
• Series Page
• Title Page
• Copyright Page
• Contents
• Preface
• Entering the terrain
• Getting ready to act
• Snapshot 1 – Capturing numbers
• Snapshot 2 – Departing from base-ten: On decimal and non-decimal representations
• Snapshot 3 – Measuring with numbers
• Snapshot 4 – Exploring variations in algorithms for arithmetic operations
• Snapshot 5 – Cycling through numbers: Focus on repeating patterns
• Snapshot 6 – Representing numbers multiplicatively: Some topics in number theory
• Snapshot 7 – Revisiting fractions: Not just pieces of pie
• Snapshot 8 – Transitioning between numerical domains
• Snapshot 9 – Playing with numbers: Puzzles, riddles and paradoxes
• The journey continues
• Index