One-Dimensional Dynamical Systems

An Example-Led Approach

Ana Rodrigues

• Publisher: CRC Press
• Year: 2021
• Print ISBN: 9780367701109
• eBook ISBN: 9781000428025
• Edition: 1
• Topic: Physical Sciences
• Subtopic: Applied Mathematics

For almost every phenomenon in physics, chemistry, biology, medicine, economics, and other sciences, one can make a mathematical model that can be regarded as a dynamical system. One-Dimensional Dynamical Systems: An Example-Led Approach seeks to deep-dive into ? standard maps as an example-driven way of explaining the modern theory of the subject in a way that will be engaging for students.

Features

• 
  
  

• Example-driven approach

• 
  
  

• Suitable as supplementary reading for a graduate or advanced undergraduate course in dynamical systems

CHAPTER 1

Introduction

For almost every phenomenon from physics, chemistry, biology, medicine, economics and other sciences one can make a mathematical model that can be regarded as a dynamical system.

Our goal is to understand the eventual or asymptotic behaviour of an iterative process.

If this process is a differential equation whose independent variable is time, then the theory aims to predict the behaviour of solutions of the equation when either $t\to \infty$ or $t\to -\infty$.

When studying discrete dynamical systems, we are interested in investigating the sequence of iterates

$$\begin{array}{l}\underset{n\text{times}}{\underbrace{x_0,f(x_0),f(f(x_0)),\dots }}.\hfill \end{array}$$

The main questions we are going to deal with are whether the system exhibits chaotic behaviour or whether it is periodic.

Let us start by introducing some basic concepts that we will use throughout this book.

We say a point x_f is a fixed point for our function f if $f(x_f)=x_f$.

The forward orbit of a point x is the set of points $x,f(x),f^2(x),f^3(x),\dots$ (note that here $f^n(x)$ denotes the nth-iterate of our function) and we usually denote this orbit by ${\mathcal{O}}^{+}(x)$. When f is a homeomorphism we can define the full orbit of our point x as the set of points $f^n(x)$ for $x\in \mathbb{Z}$. The same way we can think about the backward orbit of our point x and we denote it by ${\mathcal{O}}^{-}(x)$.

An important concept in dynamical systems are the periodic points. A point x is said periodic of period n if $f^n(x)=x$. The least positive n for which this relation holds is called the prime period of x. We will refer to the set of periodic points of period n by ${\text{Per}}_n(f)$.

We can also talk about eventually periodic points, this occurs when there exists a natural number $m>0$ such that $f^{n+i}(x)=f^i(x)$ for all $i\le m$) (in a sense $f^i(x)$ is periodic of period n for $i>m$).

Finally, we say that a point x is forward asymptotic to p if

$$\begin{array}{l}\underset{t\to \infty }{\lim }{f}^{in}(x)=p.\hfill \end{array}$$

Here it is important to note that the stable set of p is the set of all points that are forward asymptotic to p and we usually designate it by $W^s(p)$.

Let us see what happens to the map $f(x)=x^2-1$ (see Figure 1.1). To find the fixed points, we must solve the equation $f(x)=x$, that is, the quadratic equation $x^2-1=x$ which gives us the fixed points $x=1\pm \sqrt{5}/2$. Now, we have $f(-1)=0$ and $f(f(-1))=f(0)=-1$ so it is clear that $-1$ is a periodic point for f of period 2.

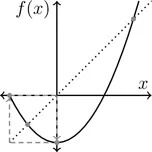
Figure 1.1: Plot of the map $f(x)=x^2-1$. The diagonal has been drawn in to illustrate the positions of the fixed points at $x=(1\pm \sqrt{5})/1$ (that lie along the diagonal) and the path of the periodic points as a web diagram $x=-1,0$ under iteration.

Another important concept is the one of the critical point. These are the points where the first derivative vanishes, this is, the points x such that $f^{\prime }(x)=0$. If we consider again the function $f(x)=x^2-1$, we see that $f^{\prime }(x)=2x$ and so, 0 is a critical point for thi...

Table of contents

• Cover
• Half Title
• Title
• Copyright
• Contents
• Chapter 1 Introduction
• Chapter 2 Rotation numbers
• Chapter 3 Topological conjugacy
• Chapter 4 Critical points
• Chapter 5 Topological theory of chaos
• Chapter 6 Symbolic dynamics
• Chapter 7 Tongues
• Bibliography
• Index