Soft Computing Approach for Mathematical Modeling of Engineering Problems

Ali Ahmadian, Soheil Salahshour, Ali Ahmadian, Soheil Salahshour

• Publisher: CRC Press
• Year: 2021
• eBook ISBN: 9781000432466
• Topic: Informatica
• Subtopic: Matematica applicata

This book describes different mathematical modeling and soft computing techniques used to solve practical engineering problems. It gives an overview of the current state of soft computing techniques and describes the advantages and disadvantages of soft computing compared to traditional hard computing techniques. Through examples and case studies, the editors demonstrate and describe how problems with inherent uncertainty can be addressed and eventually solved through the aid of numerical models and methods. The chapters address several applications and examples in bioengineering science, drug delivery, solving inventory issues, Industry 4.0, augmented reality and weather forecasting. Other examples include solving fuzzy-shortest-path problems by introducing a new distance and ranking functions. Because, in practice, problems arise with uncertain data and most of them cannot be solved exactly and easily, the main objective is to develop models that deliver solutions with the aid of numerical methods. This is the reason behind investigating soft numerical computing in dynamic systems. Having this in mind, the authors and editors have considered error of approximation and have discussed several common types of errors and their propagations. Moreover, they have explained the numerical methods, along with convergence and consistence properties and characteristics, as the main objectives behind this book involve considering, discussing and proving related theorems within the setting of soft computing. This book examines dynamic models, and how time is fundamental to the structure of the model and data as well as the understanding of how a process unfolds
• Discusses mathematical modeling with soft computing and the implementations of uncertain mathematical models
• Examines how uncertain dynamic systems models include uncertain state, uncertain state space and uncertain state's transition functions
• Assists readers to become familiar with many soft numerical methods to simulate the solution function's behavior
This book is intended for system specialists who are interested in dynamic systems that operate at different time scales. The book can be used by engineering students, researchers and professionals in control and finite element fields as well as all engineering, applied mathematics, economics and computer science interested in dynamic and uncertain systems.

Ali Ahmadian is a Senior Lecturer at the Institute of IR 4.0, The National University of Malaysia.
Soheil Salahshour is an associate professor at Bahcesehir University.

1 Soft Computing Techniques: An Overview

Morteza Pakdaman¹, Ali Ahmadian² and Soheil Salahshour³

¹Disasters and Climate Change Group, Climatological Research Institute (CRI), Atmospheric Science and Meteorological Research Center (ASMERC), Mashhad, Iran

²Institute of IR 4.0, The National University of Malaysia, Bangi, 43600 UKM, Selangor, Malaysia

³Faculty of Engineering and Natural Sciences, Bahcesehir University, Istanbul, Turkey

1.1 Introduction

In the purview of the rapidly increasing complexity, size of data and uncertainty in real-world problems in various fields such as economy, environment, engineering, science, medicine, we need suitable tools for modeling the phenomena in our daily life. On the other hand, the increase in growth of data production caused many problems in the face of data analysis, forecasting and knowledge extraction due to voluminous data.

Soft computing is a flexible tool for modeling real-world phenomena. This flexibility supports both the computational complexity and uncertainty aspects of real-world phenomena. The two main factors that led to the growth of soft computing were the development of computational methods and development of computer hardware. In the field of method development, in addition to deepening and generalization of existing methods, new approaches were created in the face of computational complexity and uncertainty of real-world problems. In the field of uncertainty and its modeling, we can refer to fuzzy logic (Zadeh 1965) and the theory of possibility (Zadeh 1978), and in the field of dealing with computational complexity, we can refer to the theory of deep learning (e.g., see Lecun et al. 2015). With the advent of computers and rapid advances in the production of supercomputers and computing systems, the knowledge of soft computing grew rapidly. This growth has been achieved in both the creation of new algorithms and approaches as well as the deepening of existing methods.

As it can be observed in Figure 1.1, the main components of real-world problems are complexity, uncertainty, scale largeness and using optimization. Soft computing can adapt itself to the main components of real-world problems by several tools, which will be discussed in this chapter.

Figure 1.1 Soft computing is a flexible tool for modeling the real-world phenomena.

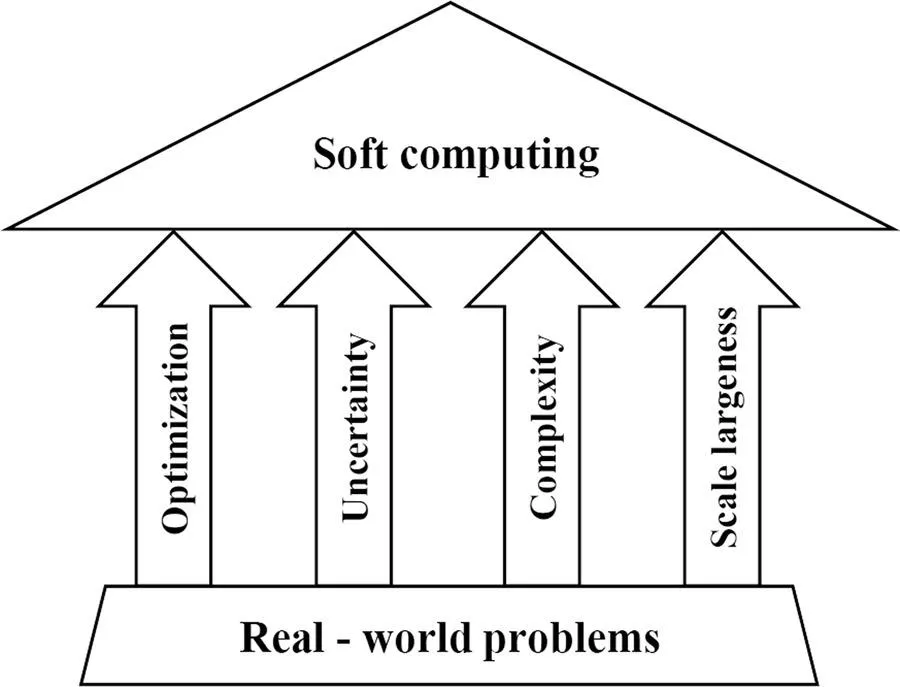
1.2 The Concept of Uncertainty: The Role of Fuzzy Logic

Uncertainty is an integral part of real-world phenomena. It is clear that in order to model a real phenomenon, its uncertainty cannot be ignored. As a rule, a good realistic modeling method should be able to model degrees of uncertainty. There are various tools for uncertainty modeling, such as probability theory and interval calculation theory (for a simple application see Effati and Pakdaman 2012). Fuzzy logic is a powerful tool in modeling the uncertainty of real-world phenomena. In the field of soft computing, fuzzy logic has been able to grow significantly as a powerful tool for modeling uncertainty in the fields of economics, science, engineering, medicine and others. This theory was first proposed by Professor Zadeh in 1965 (Zadeh 1965), and since then, in addition to various generalizations, it has been able to have wide applications in various sectors.

Fuzzy logic, unlike classical logic, is a multivalued logic. Also, in fuzzy set theory, the membership degree of an element to a fuzzy set is a number between zero and one. In classical logic, however, a member may or may not belong to a set. The concept of the membership function is used in order to calculate and present the membership degree of an element to a fuzzy set. There are several types of membership functions. In Figure 1.2, two conventional fuzzy membership functions are depicted.

Figure 1.2 Triangular (left) and trapezoidal (right) fuzzy membership functions.

In the field of applications of fuzzy logic in mathematical models and concepts, we can refer to Effati and Pakdaman (2010) where the authors presented an artificial neural network approach for solving fuzzy differential equations. Effati et al. (2011) introduced a fuzzy neural network model for solving fuzzy linear programming problems. In this paper, they presented fuzzy shortest path problems as well as fuzzy maximum flow problems. Another important application of the fuzzy set theory was for the approximation theory. Pakdaman and Effati (2016a) employed the fuzzy systems for approximating the solution of optimal control models.

From practical applications point of view, the applications of fuzzy logic cannot be limited to special cases. The use of fuzzy logic can be seen in a wide variety of practical applications such as economy, medicine, science, decision making, psychology and engineering. For example, we can refer to Hadi Sadoghi Yazi (2008) where the authors employed the concept of fuzzy uncertainty to model fuzzy current and fuzzy voltage for an electrical circuit. Dong et al. (2020) proposed a fuzzy best–worst method (BWM for short) based on triangular fuzzy numbers for multicriteria decision-making. Ren et al. (2020) proposed a multicriterion decision-making method based on the Dempster–Shafer (DS) theory and generalized Z-numbers. A Z-number is an ordered pair composed of two fuzzy numbers and DS theory is a tool for modeling uncertain information and provides weaker conditions than the traditional Bayes reasoning approach. They applied their approach to medicine selection for the patients with mild symptoms of the COVID-19. Some other applications of fuzzy logic in medicine can be found in Uzun Ozsahin et al. (2020). For the applications of fuzzy logic in the economy, we can refer to Padilla-Rivera et al. (2020) where the authors proposed an approach to identify key social indicators of circular economy (CE) through qualitative (Delphi) and quantitative (fuzzy logic) tools that objectively account for the uncertainty associated with data collection and judgment elicitation and a number of attributes (indicators) by considering the vagueness of the data. For another application of fuzzy logic in the economy, we can refer to Yu et al. (2020) where the authors studied the application of fractional-order chaotic system (based on the T–S fuzzy model) in the design of secure communication and its role in the construction of efficiency evaluation system for dispatching operation of energy-saving and power generation under a low carbon economy.

A general framework of a fuzzy system is depicted in Figure 1.3. Fuzzy logic is also used in several mathematical concepts. For example, we can refer to fuzzy calculus, fuzzy probability, fuzzy graph theory and fuzzy analysis. M. Pakdaman and Effati (2016b) and M. Pakdaman and Effati (2016c) defined the concept of fuzzy projection over the crisp set and also the meaning of fuzzy linear projection equation. The linear projection equation has several applications in the field of optimization and by defining the concept of fuzzy projection, the authors extended the applicability of fuzzy linear projection equation for fuzzy optimization problems. Lupulescu and O’Regan (2020) defined a new derivative concept for set-valued and fuzzy-valued functions. They employed this new derivative concept for differential and integral calculus in quasilinear metric spaces. Pakdaman et al. (2020) proposed an unsupervised kernel least mean squared algorithm for solving fuzzy differential equations. They applied the proposed solution procedure for solving the energy balance model. The proposed fuzzy energy balance model is a fuzzy initial value problem.

Figure 1.3 General structure of a fuzzy system.

1.3 The Concept of Complexity: The Role of Artificial Neural Networks

Artificial neural networks are simplified mathematical models of biological neural networks. Today, different types of neural networks are widely used in various scientific and technical fields. Artificial neural networks have different structures, topologies and models for different applications, including feedforward, recurrent, Hopfield, perceptron and convolutional neural networks (see, e.g., Haykin and Network 2004 and Hassoun 1995).

A general architecture of a multilayer ANN can be seen in Figure 1.4. The central processing unit of a neural network model can be considered as the artificial neuron. Neurons contain activation functions that can be of several types based on the under-study problem. Usually, for function approximation purposes, the sigmoid activation function is used as:

$\sigma (y)=\frac{1}{1+e^{-y}}$(1.1)

Figure 1.4 General architecture of a multilayer neural network.

The use of ANN for function approximation is based on the universal approximation theorem (Cybenko 1989).

Since there are several types of artificial neural networks (ANNs), they have a wide variety of applications in practice. For environmental sciences, the ANNs are applied for solving complicated problems arising in nature. Pakdaman Naghab et al. (2020) employed ANN and some other machine-learning techniques for lightning event prediction. Pakdaman et al. 2020) also employed the multilayer perceptron fo...

Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Dedication
• Contents
• preface
• Editor Biographies
• Contributors
• Chapter 1 Soft Computing Techniques: An Overview
• Chapter 2 Solution of Linear Difference Equation in Interval Environment and Its Application
• Chapter 3 Industrial Internet of Things and Industry 4.0
• Chapter 4 Industry 4.0 and Its Practice in Terms of Fuzzy Uncertain Environment
• Chapter 5 Consistency of Aggregation Function-Based m-Polar Fuzzy Digraphs in Group Decision Making
• Chapter 6 Path Programming Problems in Fuzzy Environment
• Chapter 7 Weather Forecast and Climate Prediction Using Soft Computing Methods
• Chapter 8 Color Descriptor for Mobile Augmented Reality
• Chapter 9 Cryptosystem for Meshed 3D through Cellular Automata
• Chapter 10 Evolutionary Computing and Swarm Intelligence for Hyper Parameters Optimization Problem in Convolutional Neural Networks
• Chapter 11 New Approach for Efficiently Computing Factors of the RSA Modulus
• Chapter 12 Vision-Based Efficient Collision Avoidance Model Using Distance Measurement
• Index