Classic Computer Science Problems in Java

David Kopec

• Publisher: Manning
• Year: 2020
• Print ISBN: 9781617297601
• eBook ISBN: 9781638356547
• Topic: Computer Science
• Subtopic: Computer Science General
• Index: Computer Science

Sharpen your coding skills by exploring established computer science problems! Classic Computer Science Problems in Java challenges you with time-tested scenarios and algorithms. Summary
Sharpen your coding skills by exploring established computer science problems! Classic Computer Science Problems in Java challenges you with time-tested scenarios and algorithms. You'll work through a series of exercises based in computer science fundamentals that are designed to improve your software development abilities, improve your understanding of artificial intelligence, and even prepare you to ace an interview. As you work through examples in search, clustering, graphs, and more, you'll remember important things you've forgotten and discover classic solutions to your "new" problems! Purchase of the print book includes a free eBook in PDF, Kindle, and ePub formats from Manning Publications. About the technology
Whatever software development problem you're facing, odds are someone has already uncovered a solution. This book collects the most useful solutions devised, guiding you through a variety of challenges and tried-and-true problem-solving techniques. The principles and algorithms presented here are guaranteed to save you countless hours in project after project. About the book
Classic Computer Science Problems in Java is a master class in computer programming designed around 55 exercises that have been used in computer science classrooms for years. You'll work through hands-on examples as you explore core algorithms, constraint problems, AI applications, and much more. What's inside Recursion, memoization, and bit manipulation
Search, graph, and genetic algorithms
Constraint-satisfaction problems
K-means clustering, neural networks, and adversarial search About the reader
For intermediate Java programmers. About the author
David Kopec is an assistant professor of Computer Science and Innovation at Champlain College in Burlington, Vermont. Table of Contents 1 Small problems
2 Search problems
3 Constraint-satisfaction problems
4 Graph problems
5 Genetic algorithms
6 K-means clustering
7 Fairly simple neural networks
8 Adversarial search
9 Miscellaneous problems
10 Interview with Brian Goetz

1 Small problems

To get started, we will explore some simple problems that can be solved with no more than a few relatively short functions. Although these problems are small, they will still allow us to explore some interesting problem-solving techniques. Think of them as a good warm-up.

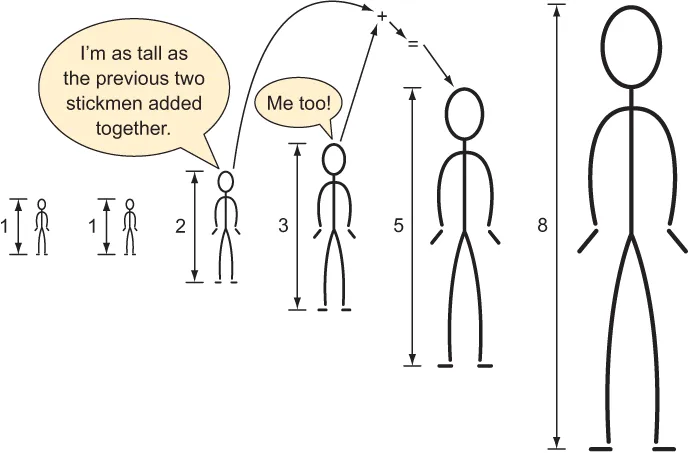
1.1 The Fibonacci sequence

The Fibonacci sequence is a sequence of numbers such that any number, except for the first and second, is the sum of the previous two:

0, 1, 1, 2, 3, 5, 8, 13, 21...

The value of the first Fibonacci number in the sequence is 0. The value of the fourth Fibonacci number is 2. It follows that to get the value of any Fibonacci number, n, in the sequence, one can use the formula

fib(n) = fib(n - 1) + fib(n - 2)

1.1.1 A first recursive attempt

The preceding formula for computing a number in the Fibonacci sequence (illustrated in figure 1.1) is a form of pseudocode that can be trivially translated into a recursive Java method. (A recursive method is a method that calls itself.) This mechanical translation will serve as our first attempt at writing a method to return a given value of the Fibonacci sequence.

Figure 1.1 The height of each stickman is the previous two stickmen’s heights added together.

Listing 1.1 Fib1.java

package chapter1; public class Fib1 {  // This method will cause a java.lang.StackOverflowError private static int fib1(int n) { return fib1(n - 1) + fib1(n - 2); }

Let’s try to run this method by calling it with a value.

Listing 1.2 Fib1.java continued

 public static void main(String[] args) {  // Don't run this! System.out.println(fib1(5)); } }

Uh-oh! If we try to run Fib1.java, we generate an exception:

Exception in thread "main" java.lang.StackOverflowError

The issue is that fib1() will run forever without returning a final result. Every call to fib1() results in another two calls of fib1() with no end in sight. We call such a circumstance infinite recursion (see figure 1.2), and it is analogous to an infinite loop.

Figure 1.2 The recursive function fib(n) calls itself with the arguments n-1 and n-2.

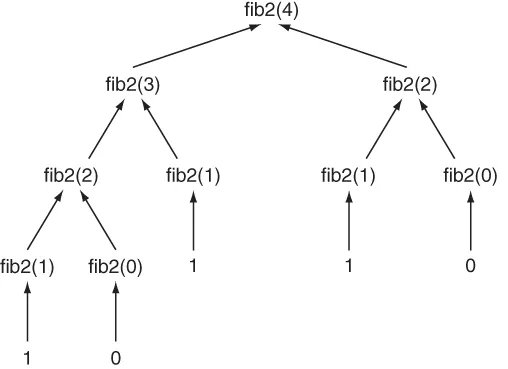
1.1.2 Utilizing base cases

Notice that until you run fib1(), there is no indication from your Java environment that there is anything wrong with it. It is the duty of the programmer to avoid infinite recursion, not the compiler. The reason for the infinite recursion is that we never specified a base case. In a recursive function, a base case serves as a stopping point.

In the case of the Fibonacci sequence, we have natural base cases in the form of the special first two sequence values, 0 and 1. Neither 0 nor 1 is the sum of the previous two numbers in the sequence. Instead, they are the special first two values. Let’s try specifying them as base cases.

Listing 1.3 Fib2.java

package chapter1; public class Fib2 { private static int fib2(int n) { if (n < 2) { return n; } return fib2(n - 1) + fib2(n - 2); }

Note The fib2() version of the Fibonacci method returns 0 as the zeroth number (fib2(0)), rather than the first number, as in our original proposition. In a programming context, this kind of makes sense because we are used to sequences starting with a zeroth element.

fib2() can be called successfully and will return correct results. Try calling it with some small values.

Listing 1.4 Fib2.java continued

 public static void main(String[] args) { System.out.println(fib2(5)); System.out.println(fib2(10)); } }

Do not try calling fib2(40). It may take a very long time to finish executing! Why? Every call to fib2() results in two more calls to fib2() by way of the recursive calls fib2(n - 1) and fib2(n - 2) (see figure 1.3). In other words, the call tree grows exponentially. For example, a call of fib2(4) results in this entire set of calls:

fib2(4) -> fib2(3), fib2(2) fib2(3) -> fib2(2), fib2(1) fib2(2) -> fib2(1), fib2(0) fib2(2) -> fib2(1), fib2(0) fib2(1) -> 1 fib2(1) -> 1 fib2(1) -> 1 fib2(0) -> 0 fib2(0) -> 0

Figure 1.3 Every non-base-case call of fib2() results in two more calls of fib2().

If you count them (and as you will see if you add some print calls), there are 9 calls to fib2() just to compute the 4th element! It gets worse. There are 15 calls required to compute element 5, 177 calls to compute element 10, and 21,891 calls to compute element 20. We can do better.

1.1.3 Memoization to the rescue

Memoization is a technique in which you store the results of computational tasks when they are completed so that when you need them again, you can look them up instead of needing to compute them a second (or millionth) time (see figure 1.4).1

Figure 1.4 The human memoization machine

Let’s create a new version of the Fibonacci method that utilizes a Java map for memoization purposes.

Listing 1.5 Fib3.java

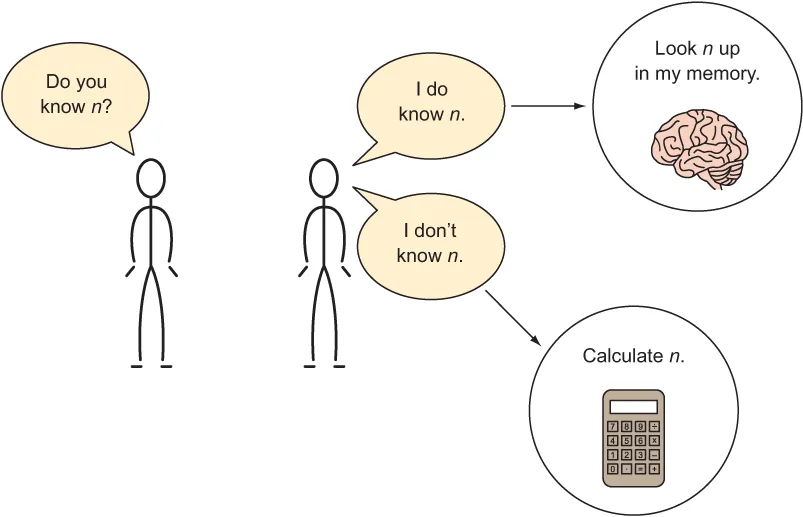
package chapter1; import java.util.HashMap; import java.util.Map; public class Fib3 {  // Map.of() was introduced in Java 9 but returns  // an immutable Map  // This creates a map with 0->0 and 1->1  // which represent our base cases static Map<Integer, Integer> memo = new HashMap<>...

Table of contents

• Classic Computer Science Problems in Java
• Copyright
• contents
• front matter
• Introduction
• 1 Small problems
• 2 Search problems
• 3 Constraint-satisfaction problems
• 4 Graph problems
• 5 Genetic algorithms
• 6 K-means clustering
• 7 Fairly simple neural networks
• 8 Adversarial search
• 9 Miscellaneous problems
• 10 Interview with Brian Goetz
• Appendix A. Glossary
• Appendix B. More resources
• index