Teaching Number

Advancing Children′s Skills and Strategies

Robert J Wright, Garry Stanger, Ann K Stafford, James Martland

• Publisher: SAGE Publications Ltd
• Year: 2006
• Print ISBN: 9781412921855, 9781412921848
• eBook ISBN: 9781446237571
• Edition: 2
• Topic: Education
• Subtopic: Teaching Mathematics

The book lets teachers identify where their students are in terms of number skills, and sets out a strategy for developing their knowledge. The authors show how to advance children?s learning across five stages of early arithmetical learning - emergent, perceptual, figurative, initial number, and facile number. This provides for increasingly sophisticated number strategies across addition, subtraction, multiplication and division, as well as developing children?s number word and numeral knowledge, and their ability to structure number and have grouping strategies. The approach used nine guiding principles for teaching.

Each chapter has clearly defined teaching procedures which show how to take the children onto the next more sophisticated stage. The teaching procedures are organized into key teaching topics, and each includes:

• a clearly defined purpose
• detailed instructions, activities, learning tasks and reinforcing games
• lists of responses which children may make
• application in whole class, small group and individualised settings
• a link to the Learning Framework in Number (see Early Numeracy- second edition, 2005)
• how the guiding principles for teaching can be used to allow teachers to evaluate and reflect upon their practice

Primary practitioners in Australia, the United States, the United Kingdom and Canada have tested the teaching procedures which can be used in conjunction with each country?s numeracy strategy.

Primary teachers, especially of the early years, mathematics co-ordinators, heads of school, mathematics advisers, special educationalists, learning support personnel, teacher assistants, lecturers in initial teacher training and educational psychologists will all find this book invaluable.

1

Advancing Children’s Strategies and Knowledge in Early Number

This chapter consists of an introductory section and two main sections. In the introductory section we describe how we use terms such as ‘strategies’ and ‘knowledge’ in describing children’s early number learning. In the first main section we describe the Learning Framework in Number which guides our assessment and the ways we observe and describe children’s learning in early number. Finally, the second main section focusses on our approach to teaching early number.

CHILDREN’S STRATEGIES AND KNOWLEDGE

This section provides an explanation of how we use terms such as ‘strategies’ and ‘knowledge’ in describing how we understand and characterize children’s learning of early number.

Children’s Strategies in Early Number

In referring broadly to children’s learning of early number we find it useful to use the terms ‘strategies’ and ‘knowledge’. The term ‘strategies’ refers to the procedures that a child might use to solve various kinds of early number tasks. Of course, there is a multitude of strategies used by children in early number learning, and any particular child might use a wide range of strategies. One can also determine differences among strategies in terms of their mathematical sophistication. Related to this, advancement in the sense of developing more sophisticated strategies is an important part of learning mathematics. Thus it follows that, in studying early number learning, it is important to focus on the strategies children use. At the same time we believe that a focus on children’s strategies alone cannot lead to fully understanding early number learning. Progression in early number learning should not be viewed only as involving the development of new strategies that an adult might classify as ‘more efficient’ than earlier strategies. Our view is that knowing the strategies that a child uses to solve early number tasks provides an important indication of the current levels of the child’s learning but does not comprehensively describe the child’s learning.

Children’s Early Number Knowledge

We use the term ‘knowledge’ to encompass aspects of children’s early number learning that we consider somewhat separate from the children’s strategies. The child, who can easily read 2-digit numerals for example, has developed important early number knowledge. This is a straightforward example of an aspect of the child’s knowledge that cannot simply be described or captured by describing a strategy the child uses to solve a problem.

Using the Term ‘Knowledge’ in an All-Encompassing Sense

In our work focussing on learning and teaching early number we use the term ‘knowledge’ in two senses. The first of these is the one just described, that is, aspects of children’s learning that are not easily characterized as strategies. Second, we use the term ‘knowledge’ in a broad and all-encompassing sense. Put simply, the knowledge that this child has in the area of early number consists of everything that the child knows about early number. This seemingly circular definition of ‘knowledge’ (that is, defining the child’s knowledge as what the child knows) is useful we believe. Thus the numerical knowledge of a 7-year-old might include aspects such as: (a) using advanced counting strategies (counting-on and counting-back) to solve additive and subtractive tasks; (b) reading and writing all 2-digit numerals and many 3-digit numerals; (c) knowing some basic addition facts (for example, doubles); and (d) counting by twos, fives and tens.

Knowledge and Learning

‘Knowledge’ used in the sense just described differs from that seen in some curriculum documents where ‘knowledge’ is used as one of three terms to encompass learning, that is ‘knowledge, skills and understandings’. Thus our use of ‘knowledge’ is likely to encompass skills and understandings. The use of the term ‘understand’ as in, for example, ‘the child understands addition’ is problematic we believe, simply because there are many levels of understanding of mathematical processes such as addition. Finally, we do not focus on a distinction between ‘concepts’ and ‘procedures’. Our view is that, at least in the area of early number learning, concepts and procedures are closely interrelated. We view a child’s concept of addition for example, primarily in terms of the strategies or procedures that the child uses in additive situations. Thus from our point of view, it makes sense to talk about a child’s knowledge of addition. This might include the range of strategies the child might use in additive situations and the sense the child might make of the symbol ‘+’. What follows, which is critical for teaching, is to learn as much as possible about the child’s current knowledge in early number and to do this it is necessary to observe closely children’s words and actions in appropriate mathematical contexts. Observing children for the purpose of learning about their current number knowledge often requires the teacher to decentre, that is, to step out of their current framework for viewing mathematics and its learning. Finally, our view of knowledge and learning in early number is strongly constructivist (von Glasersfeld, 1995), and we advocate a problem-based or inquiry-based approach to teaching (Cobb and Bauersfeld, 1995).

THE LEARNING FRAMEWORK IN NUMBER

In the Introduction we described how the ideas presented in this book are based on our work with literally thousands of teachers on three continents. In working with these teachers we first introduce them to an approach to assessment and the LFIN which provides a blueprint for the assessment and indicates likely paths for children’s learning. In this section we provide a brief description of key aspects of the LFIN. These are described in more detail in the authors’ previous book, that is, the revised edition of Early Numeracy: Assessment for Teaching and Intervention (ENATI) (Wright et al., 2006). As well, many of these ideas are revisited from a perspective of instruction, in later chapters of this book. An overview of the LFIN is provided in Table 1.1.

Table 1.1 The Learning Framework in Number

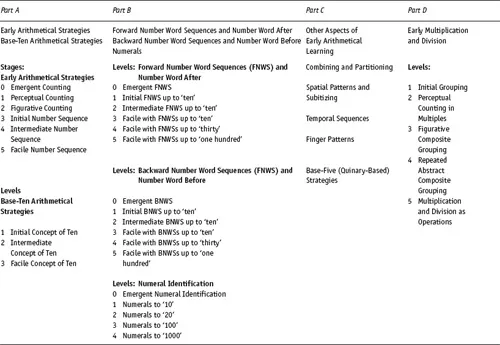
LFIN – an Overview

The LFIN contains 11 aspects of early number learning organized into four parts. Parts A, B and D contain six aspects, each of which is presented in tabular form. These tabulated forms – referred to as models – set out stages or levels of children’s numerical knowledge and facilitate profiling of children’s knowledge. The 11 aspects of the LFIN should not be regarded as early number topics which are widely separated from each other. Rather, they are closely interrelated. Thus assessing one aspect typically provides information about other aspects. Also, teaching typically focusses on several aspects simultaneously rather than just one aspect.

LFIN: Part A

Aspect A1: Stages of Early Arithmetical Learning (SEAL)

The SEAL sets out a progression of the strategies children use in early number situations which are problematic for them, for example being required to figure out how many in a collection, and various kinds of additive and subtractive situations. The SEAL model appears in Table 1.2 and consists of a progression of five stages in children’s development of early arithmetical strategies. The label ‘Stage 0’ is used for children who have not attained the first stage. The SEAL model has been adapted from research by Steffe and colleagues (for example, Steffe, 1992; Steffe and Cobb, 1988; Steffe et al., 1983) and related research by Wright (1989; 1991a). The SEAL model is considered the primary or most important aspect of the LFIN. Extensive descriptions and examples of the SEAL are available in the previous book (ENATI, 2nd edition) and so are not repeated here. Teaching procedures relating to this aspect of the LFIN appear in Key Topics 5.3 (Chapter 5), 6.3 (Chapter 6), and 7.3 (Chapter 7).

Table 1.2 Model for Stages of Early Arithmetical Learning (SEAL)

---

Stage 0: Emergent Counting. Cannot count visible items. The child either does not know the number words or cannot coordinate the number words with items.

Stage 1: Perceptual Counting. Can count perceived items but not those in screened (that is concealed) collections. This may involve seeing, hearing or feeling items.

Stage 2: Figurative Counting. Can count the items in a screened collection but counting typically includes what adults might regard as redundant activity. For example, when presented with two screened collections, told how many in each collection, and asked how many counters in all, the child will count from ‘one’ instead of counting-on.

Stage 3: Initial Number Sequence. Child uses counting-on rather than counting from ‘one’, to solve addition or missing addend tasks (e.g. 6 + x = 9). The child may use a count-down-from strategy to solve removed items tasks (e.g. 17 – 3 as 16, 15, 14 – answer 14) but not count-down-to strategies to solve missing subtrahend tasks (e.g. 17 – 14 as 16, 15, 14 – answer 3).

Stage 4: Intermediate Number Sequence. The child counts-down-to to solve missing subtrahend tasks (e.g. 17 – 14 as 16, 15, 14 – answer 3). The child can choose the more efficient of count-down-from and count-down-to strategies.

Stage 5: Facile Number Sequence. The child uses a range of what are referred to as non-count-by-ones strategies. These strategies involve procedures other than counting-by-ones but may also involve some counting-by-ones. Thus in additive and subtractive situations, the child uses strategies such as compensation, using a known result, adding to ten, commutativity, subtraction as the inverse of addition, awareness of the ‘ten’ in a teen number.

---

Aspect A2: Base-Ten Arithmetical Strategies

Around the time they attain Stage 3, 4 or 5 on the SEAL, children typically begin to develop knowledge of the tens and ones structure of the numeration system. Of course, children can and should solve addition and subtraction tasks involving 2-digit numbers (that is from 10 onward) long before they develop knowledge of the tens and ones structure. For children who have attained Stage 5, development of knowledge of the tens and ones structure becomes increasingly important. Table 1.3 outlines a progression of three levels in children’s development of base-ten arithmetical strategies. The model for the development of base-ten arithmetical strategies is adapted from research by Cobb and Wheatley (1988). Teaching procedures relating to this aspect of the LFIN appear in Key Topics 8.3 (Chapter 8), 9.3 (Chapter 9) and 9.4 (Chapter 9).

LFIN – Part B

The three aspects in Part B are concerned with important specific aspects of children’s early number knowledge: forward number word sequences, backward number word sequences, and numeral identification. These models resulted from research by Wright (for example, 1991b; 1994).

Table 1.3 Model for development of base-ten arithmetical strategies

---

Level 1: Initial Concept of Ten. The child does not see ten as a unit of any kind. The child focusses on the individual items that make up the ten. In addition or subtraction tasks involving tens, children count forward or backward by ones.

Level 2: Intermediate Concept of Ten. Ten is seen as a unit composed of ten ones. The child is dependent on re-presentations (like a mental replay or recollection) of units of ten such as hidden ten-strips or open hands of ten fingers. The child can perform addition and subtraction tasks involving tens where these are presented with materials such as covered strips of tens and ones. The child cannot solve addition and subtraction tasks involving tens and ones when presented as written number sentences.

Level 3: Facile Concept of Ten. The child can solve addition and subtraction tasks involving tens and ones without using materials or re-presentations of materials. The child can solve written number sentences involving tens and ones by adding or subtracting...

Table of contents

• Cover Page
• Title
• Copyright
• Dedication
• Contents
• List of Figures
• List of Photographs
• List of Tables
• Contributors
• Acknowledgments
• Series Preface
• Preface
• Introduction
• 1 Advancing Children’s Strategies and Knowledge in Early Number
• 2 Individualized Teaching in Mathematics Recovery
• 3 Whole-Class Teaching
• 4 General Introduction to Chapters 5 to 9
• 5 Teaching the Emergent Child
• 6 Teaching the Perceptual Child
• 7 Teaching the Figurative Child
• 8 Teaching the Counting-On Child
• 9 Teaching the Facile Child
• Bibliography
• Index