Puzzle-Based Learning (3rd Edition)

An Introduction to Critical Thinking, Mathematics, and Problem Solving

Zbigniew Michalewicz, Matthew Michalewicz

• Publisher: Credibility Corporation Pty Ltd
• Year: 2014
• eBook ISBN: 9780992286187
• Edition: 1
• Topic: Education
• Subtopic: Education Theory & Practice

What is missing in most curricula - from elementary school all the way through to university education - is coursework focused on the development of problem-solving skills. Most students never learn how to think about solving problems. Besides being a lot of fun, a puzzle-based learning approach also does a remarkable job of convincing students that (a) science is useful and interesting, (b) the basic courses they take are relevant, (c) mathematics is not that scary (no need to hate it!), and (d) it is worthwhile to stay in school, get a degree, and move into the real world which is loaded with interesting problems (problems perceived as real-world puzzles).

1The Problem: What are you after?

“I confess that I can make neither head nor tail of it. Don’t you think that you have kept up your mystery long enough, Mr. Holmes?”

Silver Blaze

---

To illustrate one of the main points of this chapter, let us introduce the first puzzle:

Puzzle 1.1

At six o’clock in the morning the wall clock struck 6 times and the time between the first and last strokes was 30 seconds. How long will the clock take to strike 12 times at noon?

It seems that one can answer this puzzle without much thought. If 6 strikes take 30 seconds, then a single strike “takes” 5 seconds. Hence 12 strikes will take 12 × 5 = 60 seconds, a full minute. Right? Well, not exactly. Problem-solving activities require some reasoning skills (and this is what this book is about), and the first skill required is the ability to understand the problem (which is the theme of this chapter).

Actually, the problem is not that easy: as a matter of fact, if we do not make any additional assumptions, there would be no unique solution! Simple (but careful) reasoning should convince us that this is the case. To start with, note that between any two consecutive strikes there is a break. So if the clock struck 6 times, then the time between the first and last strokes in the puzzle is really the total of: (a) the time for all 6 strokes, and (b) the time for 5 breaks in between strokes. If x and y represent the times required for a single stroke and for a break in between two strokes, respectively, then the information given in this puzzle can be written as:

6x + 5y = 30

The question is, on the other hand, how long will the clock take to strike 12 times? As there would be 11 breaks in the sequence of 12 strokes, the equation is:

12x + 11y = ?

Of course, the first equation leads us to the following:

12x + 10y = 60

so we know that the time between the first and last strokes would take more than 60 seconds (by one y, which is the time for one break), as:

12x + 11y = (12x + 10y) + y = 60 + y

If we do not know the length of a break, it would be impossible to solve the problem. For example, if it takes 1 second to strike (i.e., x = 1) then a break takes 4.8 seconds (i.e., y = 4.8) as 6x + 5y = 30. In this case, it will take 64.8 seconds for 12 strikes. If, on the other hand, it takes 2 seconds to strike (i.e., x = 2), then a break takes 3.6 seconds (i.e., y = 3.6). In this case it will take 63.6 seconds for 12 strikes. As you can see, the puzzle has many possible solutions …

To get a unique solution we have to assume something. We may, for instance, assume that the strikes take no time (i.e., x = 0). Then 5 breaks take 30 seconds, so the break between two strikes takes 6 seconds. For 12 strikes, there are 11 breaks between strikes, so it would take 66 seconds for the clock to strike 12 times.

In this puzzle it was essential to distinguish between strikes and breaks, and understand that it is not the case that a strike takes 5 seconds but rather that a break between two strikes takes 6 seconds. Without this understanding we may jump to the wrong conclusion.

The following puzzle also illustrates the process of understanding the problem:

Puzzle 1.2	You drive a car from point A to point B at a constant speed of 40 km/h, and, on arrival at point B, you immediately return to point A, but at a higher speed of 60 km/h. What was your average speed for the whole trip?

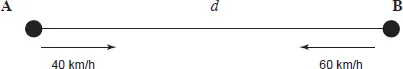The vast majority of people say that the average speed for the whole trip was 50 km/h, as they do not have a clear understanding of the term “average.” Furthermore, the correct answer of 48 km/h seems very counterintuitive to them!

How it is possible that 48 km/h is the correct answer? After all, the average of 40 and 60 is 50. To see it clearly, we have to understand the question (i.e., the problem we are trying to solve). Note that the term “average speed” is defined as a ratio between the distance and time, thus:

v_avg = D / T

where D and T represent the total distance and total time of the whole trip, respectively. There are no other definitions of “average speed” for a trip! In all circumstances, while calculating average speed, we need to know the total distance traveled and the total time for the whole trip. Other reasoning, like averaging numbers 40 km/h and 60 km/h, are simply wrong!

In our case, the total distance D is equal to 2d, where d is the distance between points A and B (as the trip takes us from point A to point B and back). On the other hand, the total time T for the whole trip consists of two components: the time t_AB to get from point A to point B and the time t_BA to get from point B to point A. Thus T is equal to t_AB + t_BA. So, the average speed for the whole trip is given as a ratio:

v_avg = D/T = 2d /( t_AB + t_BA)

How long would it take us to drive from point A to point B if we drove at constant speed of 40 km/h? Note that the travel time is a ratio between the distance and the speed, so:

t_AB = d/40

Similarly:

t_BA = d/60

With this in mind, we easily arrive at the final answer:

v_avg = 2d /( t_AB + t_BA) = 2d /( d/40 + d/60) = 2/(1/40 + 1/60) = 48

The above two puzzles illustrate the most important point in all problem-solving activities: we should have a solid understanding of the problem before we attempt to solve it! This includes understanding the concepts that we are dealing with. The term “average” is especially confusing.⁶ Consider another example that shows how important the definition of “average” is in many circumstances: There is a common perception that “we always join the slower line.” If we imagine two lines of equal length and assume that in the absence of any other information they will behave (on average) the same, then the probability of joining the slower line should be 50 percent. So where does this intuition come from? The reason is the following: the 50 percent probability of joining the slower line is an event-average, whereas the intuition above is based on the timeaverage. For example, if we calculate the probability of being in the slower line (rather than just joining it) we will (on average) spend more time in the slower line, and this time-average will result in us having a higher probability of being in this line.

So the precise definition of “average” being used in a problem is really important and not always fixed in stone (as the above example illustrated). This discussion leads us to the first rule of problem solving, which we can formulate as:

Rule #1. Be sure you understand the problem, and all the basic terms and expressions used to define it.

Note that quite often we use a variety of terms, like: “average,” “middle,” “larger,” “better,” without a proper understanding of these terms in the context of the problem at hand. Apart from understanding these terms, confusion can also arise from the way a problem (or a situation, event, etc.) is described. You have probably heard people say “the summer of 2001 was much nicer than the summer of 2002” or “the students in my class this year were smarter than the students last year.” We usually know (intuitively) what such statements mean, but upon closer inspection we might find our intuition giving way to some lingering doubts about how exactly we should interpret these sorts of claims. The following story illustrates Rule #1 very well.

Two groups of students are attending school. The students in group A boast that they are taller than the students in group B, while the students in group B enjoy the reputation of being smarter than the students in group A.

One day, one of the students from group A approached a student from group B, and said “We are taller than you!” The student from group B thought about this statement and replied: “What do you mean that statement? Do you mean that:⁷

1.Each a is taller than each b?

2.The tallest a is taller than the tallest b?

3.Each a is taller than some b?

4.Each b is smaller than some a?

5.Each a has a corresponding b (and each of them a different one) whom he surpasses in height?

6.Each b has a corresponding a (and e...

Table of contents

• Cover
• Title
• Copyright
• Foreword
• Dedication
• Preface
• Contents
• Introduction
• Part I:: Rules 1 – 2 – 3
• 1. The Problem: What are you after?
• 2. Intuition: How good is it?
• 3. Modeling: Let’s think about the problem a bit more
• Part II Mathematical Principles and Problem Types
• 4. Some Mathematical Principles
• 5. Constraints: How old are my children?
• 6. Optimization: What is the best arrangement?
• 7. Probability: Coins, dice, boxes, and bears
• 8. Statistically Speaking
• 9. Let’s Simulate!
• 10.  Pattern Recognition: What is next?
• 11  Strategy: Shall we play?
• PART III: Puzzles and Assignments
• 12  A Smorgasbord of Various Puzzles
• 13  A Smorgasbord of Various Assignments
• Concluding Remarks
• References
• Index