Advanced Common Core Math Explorations

Factors and Multiples (Grades 5-8)

Jerry Burkhart

• Publisher: Routledge
• Year: 2021
• Print ISBN: 9781618212610
• eBook ISBN: 9781000492729
• Edition: 1
• Topic: Education
• Subtopic: Teaching Mathematics

Students become mathematical adventurers in these challenging and engaging activities designed to deepen and extend their understanding of concepts from the Common Core State Standards in Mathematics. The investigations in this book stretch students' mathematical imaginations to their limits as they explore mystifying patterns of colored blocks, analyze paths of pool balls, solve mathematical word puzzles, and unravel a baffling mathematical code. Each activity comes with detailed support for classroom implementation including learning goals, discussion guides, detailed solutions, and suggestions for extending the investigation. There is also a free supplemental e-book offering strategies for motivation, assessment, parent communication, and suggestions for using the materials in different learning environments.Grades 5-8

Exploration 1
Building Blocks

DOI: 10.4324/9781003232742-3

INTRODUCTION

Materials

• » Colored pencils

Prior Knowledge

• » Identify and find factors and multiples of one- and two-digit numbers.
• » Understand the concept of a prime number (optional, but recommended).

Learning Goals

• » Understand prime numbers as building blocks of the natural (counting) numbers.
• » Analyze connections between prime factorizations of different numbers.
• » Analyze and extend complex patterns.
• » Persist in solving challenging problems.

Teacher's Note. This activity may be used to teach the concept ot prime factorization before introducing procedures such as using factor trees. If students already know about prime factorizations, this activity will give them a chance to explore the concept in more depth.

Launching the Exploration

Motivation and purpose. To students: This exploration might not really look like mathematics to you, but actually, it's all about exploring patterns—and that's math! You will eventually discover that some of the math here is familiar, but it's hidden, and part of your job is to find it! Be prepared to see this colored-block grid again in future explorations.

Understanding the problem. Read the directions for Stage 1 to make sure students understand them, but be careful not to give anything away! Don't tell them that it is about factors, multiples, or prime numbers. They will discover this for themselves! Encourage them to record their ideas on separate "thinking" paper until they are confident in the results before transferring their work to the final copy. Offer assistance as needed for a least a few minutes as they begin the exploration to make sure they understand the main idea.

NAME:────────── DATE:─────

STUDENT HANDOUT

Stage 1

1. Analyze patterns in the colored blocks for the top 50 squares of this grid. Extend the patterns to fill in the remaining 50 squares.

Note. The goal is to figure out how many blocks of each color are in each square, not how they are arranged. (There is a pattern in the arrangement, too, but its purpose is just to make the grid easier to read.)

Stage 2

• 2. Draw the correct block pattern into the two empty squares and fill in the correct colors for all blocks in the grid. Include any additional information that you think is important.

Note. All patterns from the original grid continue to apply. But now, the arrangement of blocks within each square is important!

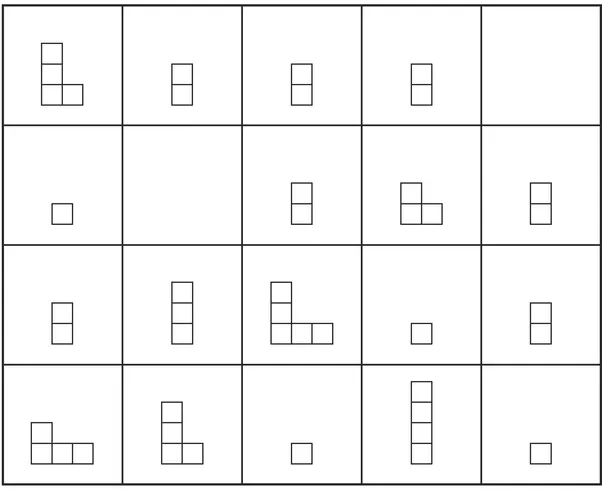
Stage 3

• 3. Look at the grid in Stage 1 and focus on the squares that have just one block. Can you find a method that will always predict when the next one will come?

TEACHER’S GUIDE

STAGE 1

Problem # 1

1. Analyze patterns in the colored blocks for the top 50 squares of this grid. Extend the patterns to fill in the remaining 50 squares.

Note. Ih e goal is to figure out how many blocks of each color are in each square, not how they are arranged. (There is a pattern in the arrangement, too, but its purpose is just to make the grid easier to read.)

Questions and Conversations for # 1

This section contains ideas for conversations, including questions that students may ask or that you may pose to them. Give them plenty of time to explore on their own before going too deeply into the questions and ideas here. Be sure that students are doing most of the thinking and talking!

• » Is it important to keep the blank square in the upper left corner? Yes. The pattern will be easier to understand if you keep it there.
• » Are there patterns in rows, columns, diagonals, etc.? Yes, there are many vertical and diagonal patterns. For example, white blocks appear in alternating columns. What pattern do you see for red blocks?
• » Does every color show some pattern? Yes, every color follows some distinctive pattern. Try to think about what might cause these patterns.
• » Will it help to count the total number of blocks in each row or column? You might make interesting observations by counting these, but it will probably not help you complete the grid.
• » Will it help to look for a pattern in the number of white blocks in the squares? It might, but it's a complicated pattern. Reading from left to right, top to bottom, it looks like this: 1, 2, 1, 3, 1, 2, 1, 4, 1,2, 1, 3, 1, 2, 1, 5, 1, 2, 1, 3, 1, 2, 1, 4,... Every natural number will eventually appear in this list! You might find the pattern hard to unravel without more information.
• » Can it help to focus on patterns in squares in which all blocks are the same color? Yes. This will probably help the most for squares with white blocks because you can't see many squares of this type for the other colors.
• » Should I look at the squares in a particular order? Yes, try reading the grid from left to right, top to bottom, just as you would read a book.
• » Will two different squares ever have exactly the same collection of colored blocks? No.

Teacher's Notes. Most students can easily spend a few days on Stage 1. If they finish while others are still working, they can continue to look for more patterns or move on to Stage 2. There are many "small" patterns that can help students fill in parts of the remaining squares. There is also one "general" pattern that ties all of the smaller patterns together.

Teacher's Note. Students often enjoy working on the 1, 2, 1, 3, 1, 2, 1, 4,... pattern, but if they have explored it for a while without success, you might suggest that they pursue other avenues. Encourage them to come back to it after they have solved the entire puzzle. By the way, other colors show similar types of complex patterns!

• » What always happens the first time a new color appears? Every color appears by itself the first time.
• » What always happens the second time a new color appearst Every color appears with a white block the second time. Can you see how this pattern continues?
• » Does the main pattern have anything to do with numbers? Yes. Try numbering the squares in order from left to right, top to bottom.
• » Should the first square be numbered "0" since it contains no blocks? This is an important question. Experiment before deciding. (It turns out that the blank square at the beginning should be numbered 1, not 0.)
• » Look at the squares numbered 2, 3, and 6 or 3, 4, and 12. What happens? Look at how the block diagrams combine. Under what circumstances does this happen in general?
• » In which square will the next white block go? What about the next red block? Students might notice that white blocks occur every 2 squares, red blocks come every 3 squares, orange ones appear every 5 squares, etc. (This is a key pattern.)
• » Once you know that a square contains a certain color, how can you figure how many blocks of that color it has? Look at the squares that have at least two white blocks. What about three white blocks? Ask the same types of questions for other colors.
• » Is there anything special about the squares with just one block? Yes! Try writing down the numbers of these squares. (These squares are all labeled as prime numbers!)

Teacher's Note. If students discover that some squares never seem to get filled with any blocks, it might be a good time to mention that new colors will sometimes be needed. When this happens, students may choose the color.

Solution for # 1

The general pattern is that the completed grid is a picture of the prime factorizations of the natural (counting) numbers from 2 through 100! (The number 1 is represented as no blocks.) Each color represents a prime number: 2 is white, 3 is red, 5 is orange, 7 is yellow, etc. Attaching the blocks represents multiplying the corresponding prime numbers.

STAGE 2

Problem #2

• 2. Draw the correct block pattern into the two empty squares and fill in the correct colors for all blocks in the grid. Include any additional information that you think is important.

Note. All patterns from the original grid continue to apply. But now, the arrangement of blocks within each square is important!

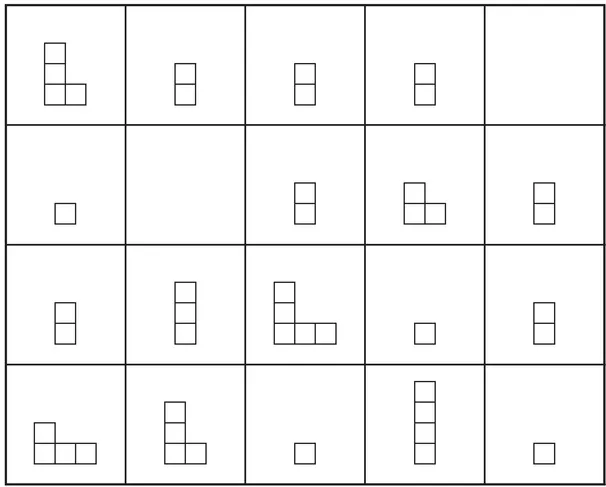
Questions and Conversations for #2

• » How are the blocks arranged in each square? Each row of blocks contains only one prime number value. The smallest prime number is i...

Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Table of Contents
• A Note to Students
• Introduction
• Connections to the Common Core State Standards
• Exploration 1: Building Blocks
• Exploration 2: 1000 Lockers
• Exploration 3: Factoring Large Numbers
• Exploration 4: Factor Scramble
• Exploration 5: How Many Factors?
• Exploration 6: Differences and Greatest Common Factors
• Exploration 7: A Measurement Dilemma
• Exploration 8: Paper Pool
• Exploration 9: The GCF-LCM Connection
• Exploration 10: Mathematical Mystery Code
• References
• About the Author
• Common Core State Standards Alignment