Alea iacta est

Faszinierende Geheimnisse eines ungewöhnlichen Spielwürfels

Peter P. Eckstein

• Publisher: UVK Verlag
• Year: 2016
• Print ISBN: 9783867647571
• eBook ISBN: 9783739802350
• Topic: Mathematics
• Subtopic: Mathematics Reference
• Index: Mathematics

Der Würfel ist gefallenErstaunliches, Faszinierendes, Skurriles und mitunter auch Mystisches rund um diesen besonderen Spielwürfel zeigt der Autor dem Leser in diesem Buch. Auf dessen sechs Seiten sind keine Augenzahlen, sondern die neutrale Zahl Null, die natürliche Zahl Eins, die irrationale Zahl Phi, die irrationalen Zahlen e und Pi sowie die imaginäre Einheit i vermerkt. Allein anhand der sechs auf diesen ungewöhnlichen Spielwürfel vermerkten Zahlen wird also eine Vielzahl von numerischen Erscheinungsbildern angeboten.Der interessierte Leser muss bei diesen Abhandlungen nicht befürchten, einen schwerverdaulichen Zahlensalat kauen und schlucken zu müssen. Im Gegenteil: Er wird mitunter erstaunt sein, wie vielfältig und faszinierend das Zusammenspiel dieser sechs Zahlen allein in alltäglichen Phänomen und praktischen Anwendungen ist. Die paradigmatischen Betrachtungen umspannen ein weites Wissensfeld, das von mathematischen über statistische, historische, literarische, musikalische, kunstgeschichtliche und sprachwissenschaftliche bis hin zu etymologischen Notizen reicht. Es steht dabei außerhalb jeglichen Zweifels, dass die vermerkten konzertanten Auftritte des Zahlensextetts wiederum nur einen Auszug aus einem schier unerschöpflichen Fundus darstellen.

1 Betrachtungen eines gewöhnlichen Spielwürfels

1.1 Interessante geometrische Einblicke

Ein Bild ersetzt mitunter viele wohlgesetzte Worte: In Anlehnung an die Abbildung 1 stelle man sich einmal vor, ein „alter Germane“ würfe einen solchen eckigen Stein.

Abb. 1: Würfeln

Beachtenswert sind in diesem Kontext zwei Notizen: Zum einen lässt sich in der deutschen Sprache das Verbum „würfeln“ als Tätigkeitswort aus dem Verbum „werfen“ herleiten, da der Konjunktiv II von „werfen“ mit „würfe“ zu vermerken ist. Zum anderen wird der geworfene und mit eingekerbten Augen gekennzeichnete eckige Stein umgangssprachlich mit dem Etikett eines Spielwürfels versehen und in der sogenannten Stereometrie der in der Abbildung 2 plakatierten Familie der fünf sogenannten regulären Polyeder zugeordnet.

Abb. 2: Die fünf regulären Polyeder

In der Stereometrie, die gemäß ihrem griechischen Wortursprung die Lehre von der Messung und Berechnung von Körpern ist, kennzeichnet man die fünf regelmäßigen Vielflächner auch als platonische Polyeder, da sie zum einen von regelmäßigen und deckungsgleichen vieleckigen Flächen begrenzt werden und zum anderen an jeder Ecke gleichviele Kanten zusammentreffen.¹

Abb. 3: Spielwürfel

Aufgrund dessen, dass analog zur Abbildung 3 ein gewöhnlicher Spielwürfel durch sechs kongruente und quadratische Flächen getragen wird, kennzeichnet man ihn in Anlehnung an das Griechische hex für „sechs“ und herda für „Fläche“ als ein Hexaeder, das als ein Sechsflächner zudem noch acht Ecken, in denen jeweils drei kongruente Quadrate zusammentreffen, und zwölf Kanten von jeweils gleicher Länge besitzt.

In diesem Zusammenhang erweist sich ein kurzer Blick auf die Briefmarke innerhalb der Abbildung 4 als interessant.

Abb. 4: Polyederformel

Es war im Jahr 1983, als die Post der DDR im Wert von 20 Pfennigen eine Briefmarke in Erinnerung an das 200 Jahre zurückliegende Todesjahr des bedeutenden Mathematikers Leonhard EULER (*1707, †1783) herausgab. Neben der geometrischen Figur eines Ikosaeders als ein Zwanzigflächner ist auf der Briefmarke die leicht zu übersehende Gleichung

vermerkt, die zu Ehren von EULER auch als Eulersche Polyederformel oder als Eulerscher Polyedersatz bezeichnet wird, gleichwohl vermutlich schon der legendäre Mathematiker der griechischen Antike ARCHIMEDES von Syrakus (*ca. 287 v.Chr., † 212 v.Chr.) und mit Gewissheit der französische Mathematiker René DESCARTES (*1596, †1650) den sogenannten Polyedersatz gekannt haben.² Demnach gilt für platonische oder reguläre Polyeder die folgende Regel: Anzahl der Ecken e minus Anzahl der Kanten k plus Anzahl der Flächen f ist gleich zwei.

Gemäß Abbildung 3 gilt für ein regelmäßiges Hexaeder in Gestalt eines gewöhnlichen sechsseitigen Spielwürfels

Die Polyederformel kann man sich auch anhand der restlichen vier regelmäßigen Vielflächner verdeutlichen. Während für ein Tetraeder als einen Vierflächner

gilt, gelangt man für ein Oktaeder als einen Achtflächner wegen

für ein Pentagondodekaeder in Gestalt eines Zwölfflächners wegen

und für ein Ikosaeder im Erscheinungsbild eines Zwanzigflächners wegen

stets zu einem gleichen Resultat. In Erinnerung an die eigene Gymnasialzeit hätte der „Mathepauker“ die fünf auf der Polyederformel beruhenden Berechnungen noch mit der Abkürzung q.e.d. geschmückt, die gemäß dem Lateinischen quod erat demonstrandum für den finalen Kommentar „was zu zeigen war“ steht.

---

¹ Zu den fünf regemäßigen Körpern oder Vielflächnern, die vermutlich in Würdigung des griechischen Philosophen PLATON (* 427 v.Chr., † 348/347 v.Chr.) auch als platonische Polyeder bezeichnet werden, gehören das Tetraeder als ein Vierflächner, das Hexaeder als ein Sechsflächner, das Oktaeder als ein Achtflächner, das Pentagondodekaeder als ein Zwölfflächner sowie das Ikosaeder als ein Zwanzigflächner. Vgl. Kleine Enzyklopädie Mathematik, VEB Bibliographisches Institut Leipzig 1977, 8.5 Polyeder, Seite 211 ff und Brockhaus Enzyklopädie in 30 Bänden, 21., völlig neu bearbeitete Auflage, Leipzig, Mannheim 2006, Band 21, Seite 558 ff

² Vgl. Kleine Enzyklopädie Mathematik, VEB Bibliographisches Institut Leipzig 1977, 8.5 Polyeder, Seite 212

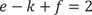
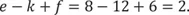
1.2 Die Augenzahlen und ihre exakten Geheimisse

Einen weiteren und nicht minder interessanten Einblick in die exakten Geheimnisse eines gewöhnlichen Spielwürfels gewährt das Ensemble der eingekerbten Augen, welche als „Augenmengen“ analog zur Abbildung 5 mit Hilfe der natürlichen Zahlen von eins bis sechs dargestellt und beschrieben werden können.

Abb. 5: Augen(an)zahlen

Beachtenswert ist dabei, dass die innerhalb der Abbildung 5 angebotene Zuordnung der ersten sechs natürlichen Zahlen auf die sechs kongruenten bzw. deckungsgleichen Flächen in Gestalt von sechs Quadraten nur eine von insgesamt 720 möglichen Anordnungen darstellt.

Im Blickwinkel der Kombinatorik, die gemäß ihrem lateinischen Wortursprung die Lehre von der Zusammenstellung von Elementen ist, kann die Anzahl der möglichen Augenzahlanordnungen als eine Permutation von sechs Elementen ohne Wiederholung dargestellt werden, wobei im konkreten Fall

gilt.³ Die verkürzende Notation 6! (lies: 6 Fakultät) in Gestalt des Produkts der natürlichen Zahlen von eins bis sechs geht auf den französischen Mathematiker Christian KRAMP (*1760, †1826) zurück.

Würde man analog zur Abbildung 5 die plakatierte Augenzahlzusammenstellung in Gestalt ...

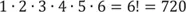
Table of contents

• Hinweise
• Vorwort
• Inhaltsverzeichnis
• 1. Betrachtungen eines gewöhnlichen Spielwürfels
• 2. Ein magisches Hexaeder
• 3. Konzertante Auftritte eines Zahlensextetts
• Epilog
• Index
• Impressum