1. Sei gradi di separazione
Molti aspetti della realtà si presentano al nostro sguardo sotto forma di reti, cioè insiemi di nodi collegati in modo più o meno fitto tra loro. Ad esempio, gli atomi dei solidi cristallini formano griglie dette «reticoli regolari», della cui struttura si conosce ormai quasi tutto. Negli ultimi decenni, le reti di origine umana hanno stimolato la curiosità intellettuale degli scienziati molto più di quelle naturali. In tutta la seconda metà del Novecento, infatti, sono stati soprattutto sociologi e matematici a elaborare i modelli teorici delle reti sociali. Solo in un secondo momento, con l’accumularsi delle osservazioni empiriche, gli scienziati si sono accorti che le proprietà delle reti sociali sono presenti in tanti altri ambiti, e il loro studio è divenuto uno degli ambiti di ricerca più fiorenti della fisica statistica.
La storia della teoria delle reti complesse, dunque, nasce con la sociologia. In una comunità, ad esempio, le persone che si conoscono formano una rete sociale. Oggi queste reti sono osservate in dettaglio in tempo reale: le relazioni personali, infatti, sempre più spesso passano in forma digitale attraverso telefoni e computer, grazie ai quali possono essere registrate e analizzate con strumenti statistici. I social network on-line registrano informazioni relative a milioni di utenti, e spesso le rendono pubbliche (garantendo la privacy) per scopi di ricerca. Per molto tempo, invece, raccogliere dati affidabili sulle reti sociali non è stato affatto facile: i sociologi si affidano tradizionalmente a interviste e questionari, e questo limita necessariamente la dimensione del campione studiato. Tuttavia, anche senza la possibilità di analizzare le banche dati oggi disponibili, alcune peculiarità delle reti sociali sono state evidenti da subito.
Innanzitutto, le reti sociali reali contengono un alto grado di disordine. Le conoscenze personali dipendono da eventi fortuiti e irripetibili, e non seguono una particolare logica: ci si conosce sulla base di un gradimento reciproco tra due persone e il resto della rete sociale influisce solo in parte sui legami tra gli individui.
Anche il secondo aspetto non richiede particolari competenze: capita infatti a chiunque, non solo agli scienziati, di esclamare «Quanto è piccolo il mondo!». Accade quando scopriamo di avere un amico (o un parente o un commercialista) in comune con un perfetto estraneo. Succede talmente spesso che sarebbe sbagliato considerarlo un evento eccezionale. Si tratta, piuttosto, di una proprietà fondamentale delle relazioni sociali: bastano pochi intermediari per mettere in contatto due persone qualunque in una popolazione di milioni, o anche miliardi, di persone. Già nel 1958, il matematico Manfred Kochen e il politologo Ithiel de Sola Pool avevano individuato nell’effetto Small World («Piccolo Mondo») la principale caratteristica delle reti sociali in un saggio intitolato «Contacts and Influence» e curiosamente pubblicato solo vent’anni dopo. Fino ad allora non esistevano dati quantitativi che lo confermassero. Fu lo psicologo Stanley Milgram, nel 1967, a dimostrare che il mondo è realmente piccolo. Milgram chiese a un gruppo di volontari residenti in Kansas e Nebraska di inviare alcune lettere in Massachusetts non attraverso il sistema postale, ma consegnandole ad amici e conoscenti che, a loro volta, avrebbero cercato nel loro entourage persone in grado di far arrivare la lettera a destinazione. Il risultato fu sorprendente: le lettere raggiungevano il destinatario usando in media solo cinque intermediari. Milgram ripeté l’esperimento in altre comunità, e l’effetto Small World fu confermato. La teoria e l’esperimento ebbero grande successo anche presso l’opinione pubblica, al punto da ispirare la commedia e il film dal titolo Sei gradi di separazione. Negli ultimi anni è stato dimostrato che in molte altre reti si può osservare l’effetto Small World: analizzando i contatti su scala mondiale tra gli utenti del programma di instant messaging Msn, si scopre che i gradi di separazione sono esattamente 6,6, come previsto; gli attori di Hollywood, connessi se hanno lavorato insieme almeno una volta, sono separati mediamente da due soli intermediari. La regola, inoltre, non vale solo per le reti sociali: anche nella rete dei server di Internet o in quella dei neuroni ci sono solo tre gradi di separazione. E la lista delle reti con pochi gradi di separazione è davvero lunga.
I grafi aleatori
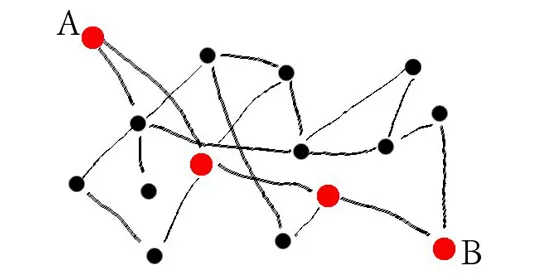
Un semplicissimo modello introdotto da Ray Solomonoff e Anatol Rapoport nel 1951 e approfondito da Paul Erdös e Alfréd Rényi (a cui è generalmente attribuito) nel 1959 sembra adatto a riprodurre le caratteristiche delle reti reali in prima approssimazione. Il modello consiste in un insieme di N punti inizialmente isolati detti «nodi», in cui alcune coppie di punti estratte a sorte vengono collegate (perciò il modello è denominato «grafo aleatorio»). Il numero di coppie collegate deve essere sufficiente a connettere l’intero sistema, in modo che per ogni coppia di punti esista una catena di legami che la unisca. I matematici dimostrarono che nei grafi aleatori la distanza media tra due nodi, denominata il «diametro» della rete, è proporzionale al logaritmo di N. Per comprendere il significato di questa legge, ricordiamo che il logaritmo (in base 10) di 100 è 2, il logaritmo di 1000 è 3, il logaritmo di 1000000 è 6: dunque, anche un grafo composto da milioni di nodi può avere un diametro pari a poche unità, e ciò spiegherebbe perché anche due abitanti di un paese grande come gli Stati Uniti siano separati da pochi intermediari (vedi figura 1).
Figura 1: A causa dell’effetto Small World, tra due nodi di una rete ci sono generalmente pochi gradi di separazione. (Immagine di A. Capocci)
Reti raggruppate
Nonostante il disordine apparente delle reti sociali reali, le relazioni tra le persone non sono del tutto indipendenti dal contesto in cui si trovano. Ad esempio, due amici solitamente hanno più amicizie in comune rispetto a due estranei. In altre parole, se due individui sono entrambi connessi a un terzo individuo, probabilmente anche tra loro c’è un legame, che dunque forma un triangolo. Questa proprietà delle reti è detta transitività o clustering, che in inglese significa raggruppamento. La società tende infatti a organizzarsi in circoli più o meno chiusi, in cui ci si conosce tutti e da cui si escludono gli esterni. Una rappresentazione realistica della società non può ignorare questo fenomeno, che dunque deve essere descritto matematicamente. La transitività si misura con un coefficiente compreso tra 0 e 1. Il valore nullo corrisponde al caso in cui nella rete non sono presenti triangoli. Per immaginare una rete di questo tipo pensiamo a un albero: i rami non si riuniscono mai dopo essersi separati, e dunque non formano triangoli. Se invece ogni coppia di nodi con un vicino in comune è a sua volta connessa, il coefficiente assume il valore massimo e la rete assomiglia a un intrico di connessioni che collega tutti i nodi a tutti gli altri. In quest’ultimo caso, dunque, due individui che hanno un amico in comune sono anche amici tra loro. Di solito, il coefficiente di transitività ha un valore intermedio. Nella rete delle collaborazioni tra attori cinematografici è pari a 0,2 e nella rete neuronale è pari a 0,18; ma nella rete più esclusiva di tutte, quella dei manager associati nei consigli di amministrazione italiani, il coefficiente di transitività balza a uno stupefacente 0,59. Nei corrispondenti grafi aleatori, costruiti con lo stesso numero di nodi e di connessioni dei casi reali, il coefficiente di transitività è praticamente nullo. Il grafo aleatorio dunque non è un modello davvero utile per rappresentare le reti sociali reali.
Il fenomeno dei sei gradi di separazione e il forte raggruppamento sono entrambi fattori che favoriscono la formazione e la stabilità delle reti: il raggruppamento facilita la coesione e l’effetto Small World velocizza lo scambio di informazioni e la velocità di adattamento. Tuttavia, sono aspetti in contraddizione tra loro: in una rete molto raggruppata, esplorando le relazioni sociali dei vicini di un nodo non ci si allontana molto dal nodo di partenza, perché gli amici degli amici sono amici tra loro; per attraversare l’intera rete con pochi gradi di separazione, invece, è necessario che i vicini di un nodo abbiano contatti con aree della rete lontane dal nodo di partenza. Il problema di conciliare entrambi gli aspetti, dunque, non è affatto banale.
Paradossalmente, per costruire una rete con transitività elevata basta un reticolo regolare. Se disponiamo i nodi su una griglia e colleghiamo ogni nodo con i suoi otto nodi più vicini (come nella figura 2a), è facile osservare che i vicini di un nodo sono collegati tra loro e formano un gran numero di triangoli. Purtroppo, questa rete non possiede l’effetto Small World: se la griglia è abbastanza estesa, i nodi ...