Reviews in Computational Chemistry, Volume 32

Abby L. Parrill, Kenny B. Lipkowitz, Abby L. Parrill, Kenny B. Lipkowitz

• Publisher: Wiley
• Year: 2022
• Print ISBN: 9781119625896
• eBook ISBN: 9781119625940
• Edition: 1
• Topic: Physical Sciences
• Subtopic: Chemistry
• Index: Chemistry

REVIEWS IN COMPUTATIONAL CHEMISTRY

THE LATEST VOLUME IN THE REVIEWS IN COMPUTATIONAL CHEMISTRY SERIES, THE INVALUABLE REFERENCE TO METHODS AND TECHNIQUES IN COMPUTATIONAL CHEMISTRY

Reviews in Computational Chemistry reference texts assist researchers in selecting and applying new computational chemistry methods to their own research. Bringing together writings from leading experts in various fields of computational chemistry, V olume 32 covers topics including global structure optimization, time-dependent density functional tight binding calculations, non-equilibrium self-assembly, cluster prediction, and molecular simulations of microphase formers and deep eutectic solvents. In keeping with previous books in the series, Volume 32 uses a non-mathematical style and tutorial-based approach that provides students and researchers with easy access to computational methods outside their area of expertise.

The chapters comprising Volume 32 are connected by two themes: methods that can be broadly applied to a variety of systems, and special considerations required when modeling specific system types. Each in-depth chapter contains background and theory, strategies for using the methods correctly, mini-tutorials and best practices, and critical literature reviews highlighting advanced applications. Essential reading for both newcomers and experts in the area of molecular modeling, this state-of-the-art resource:

• Covers topics such as non-deterministic global optimization (NDGO) approaches and excited-state dynamics calculations
• Contains a detailed overview of deep eutectic solvents (DESs) and simulation methods
• Presents methodologies for investigating chemical systems that form microphases with periodic morphologies such as lamellae and cylinders
• Features step-by-step tutorials on applying techniques to probe and understand the chemical dynamics exhibited in a system
• Includes detailed subject indices on each volume in the series and up-to-date compendiums of molecular modeling software, services, programs, suppliers, and other useful information

Reviews in Computational Chemistry, Volume 32 is a must-have guide for computational chemists, theoretical chemists, pharmaceutical chemists, biological chemists, chemical engineers, researchers in academia and industry, and graduate students involved in molecular modeling.

1
NON‐DETERMINISTIC GLOBAL STRUCTURE OPTIMIZATION: AN INTRODUCTORY TUTORIAL

BERND HARTKE

Theoretical Chemistry, Institute for Physical Chemistry, Christian‐Albrechts‐University, Olshausenstr. 40, 24098 Kiel, Germany

LIST OF ABBREVIATIONS

ACO:

Ant‐Colony Optimization

BH:

Basin Hopping (Monte Carlo with Minimization)

CD:

Collision Detection

CD/DD:

combined Collision and Dissociation Detection

CSP:

Crystal Structure Prediction

DD:

Dissociation Detection

DFT:

Density Functional Theory

DFTB:

Density Functional Tight‐Binding

DOF:

Degree of Freedom

DGO:

Deterministic Global Optimization

FF:

Force Field (empirical potential)

GA:

Genetic Algorithm

GO:

Global Optimization

HPC:

High‐Performance Computing

IR:

infrared

:

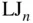
Lennard‐Jones cluster with

atoms

MC:

Monte Carlo

MCM:

Monte Carlo with Minimization (Basin Hopping)

MD:

Molecular Dynamics

ML:

Machine Learning

MP2:

Møller‐Plesset perturbation theory, second order

MPI:

message‐passing interface (parallelization)

NDGO:

Non‐Deterministic Global Optimization (algorithms)

NFL(T):

No Free Lunch (Theorem) for search and optimization

PES:

Potential Energy Surface

PSO:

Particle Swarm Optimization

SA:

Simulated Annealing

wNFL(T):

Weak No Free Lunch (Theorem)

INTRODUCTION

The Need for Structural Optimization

For any calculation of static or dynamic properties of molecular systems, the (starting) structures of these molecules need to be known, at the level of theory to be used. Since full configuration interaction in a complete basis set extrapolation (and possibly with explicitly treated solvent molecules, at finite temperature, etc.) is not practical, every level of theory is approximate, in the sense that its results differ from experimental data. Because properties may change appreciably even with small structure distortions, using experimental molecular structures is not a good idea. Instead, they always need to be optimized at the given level of theory, before any further calculations can commence.

Several decades ago, computational chemistry could only deal with small, isolated molecules. For these, local optimizations from guessed starting structures were sufficient. These starting structures could be taken from chemical intuition or from experiment. With gradients and frequencies (1st and 2nd derivatives of the electronic energy with respect to the nuclear coordinates) at the given level of theory, a local minimum‐energy^* structure can then be found, using efficient standard procedures that are general and system‐independent. This is taken for granted now, but significant development efforts were required,¹ as well as an acknowledgment of the need for all this in the computational chemistry community.

For three decades, we have experienced complex systems in theoretical calculations, giving rise to very many local minimum‐energy structures. Frequently, experimental information is insufficient to disentangle the signatures from several different species, and human chemical intuition may also struggle, at least outside the area of standard organic chemistry. In such situations, approaches are needed that can find many or all local minima and locate the best one of these, i.e., global optimization (GO).

It is frequently assumed that it may suffice to substitute true global optimization by simply performing series of local minimizations, from different guessed starting structures. However, with increasing complexity, this naive approach quickly loses any reliability. This was so well‐known in the GO community already in the 1990s that it took a surprisingly long time until Avaltroni and Corminboeuf demonstrated this explicitly for a real‐life test case² in the published literature. Until today, however, this finding frequently remains underappreciated. Astonishingly, even today, papers can be published³ in which not even the need for global structure optimization is recognized.

Search Space is Vast

This failure of series of local minimizations arises because the search space of molecular structures is huge: It scales exponentially with the number of degrees of freedom (DOF). The essence of the reason for this scaling is depicted in Figure 1.

Unless a priori information allows for general restrictions, we have to combine every possible coordinate value in one DOF with every other value in all other DOFs, in direct‐product style. This obviously leads to exponential scaling of the search space size to be covered, with the number of coordinates or particles. Thus,

scaling is a basic feature of

‐dimensional space, combined with the need to cover all of it. This need arises from our wish to be sure to find the true global minimum and from our lack of global information: Without reliable a priori information on how the function

to be optimized behaves at a new point

, we have to visit this new point (i.e., we need to evaluate

at

)—but as soon as we do this for all new points

, we are stuck in the

trap.

Figure 1 illustrates how exponential scaling arises, but fails to illustrate how bad exponential scaling really is. Because even seasoned experts sometimes underappreciate this, it is provided by Table 1, which shows linear, cubic, and exponential scaling with the number of DOFs, in terms of computational wallclock times. It starts with the assumption that a calculation for 5 DOFs needs one second, which is a completely arbitrary setting (but somewhat realistic, e.g., for quantum‐chemistry calculations). The ensuing scaling with the number of DOFs (which also is chemically realistic, for electrons or nuclei), however, is very real and shows drastically that all exponentially scaling algorithms can be used only for small DOF numbers. Obviously, this situation cann...

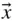
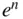
Table of contents

• Cover
• Table of Contents
• Title Page
• Copyright
• LIST OF CONTRIBUTORS
• PREFACE
• CONTRIBUTORS TO PREVIOUS VOLUMES
• 1 NON‐DETERMINISTIC GLOBAL STRUCTURE OPTIMIZATION: AN INTRODUCTORY TUTORIAL
• 2 DENSITY FUNCTIONAL TIGHT BINDING CALCULATIONS FOR PROBING ELECTRONIC‐EXCITED STATES OF LARGE SYSTEMS
• 3 ADVANCES IN THE MOLECULAR SIMULATION OF MICROPHASE FORMERS
• 4 MOLECULAR SIMULATIONS OF DEEP EUTECTIC SOLVENTS: A PERSPECTIVE ON STRUCTURE, DYNAMICS, AND PHYSICAL PROPERTIES
• INDEX
• Wiley End User License Agreement