eBook - ePub
Dynamic Systems Modelling and Optimal Control
Applications in Management Science
Victoria Miroshnik,Dipak Basu
This is a test
Share book
- English
- ePUB (mobile friendly)
- Available on iOS & Android
eBook - ePub
Dynamic Systems Modelling and Optimal Control
Applications in Management Science
Victoria Miroshnik,Dipak Basu
Book details
Book preview
Table of contents
Citations
About This Book
Dynamic Systems Modelling and Optimal Control explores the applications of oil field development, energy system modelling, resource modelling, time varying control of dynamic system of national economy, and investment planning.
Frequently asked questions
How do I cancel my subscription?
Can/how do I download books?
At the moment all of our mobile-responsive ePub books are available to download via the app. Most of our PDFs are also available to download and we're working on making the final remaining ones downloadable now. Learn more here.
What is the difference between the pricing plans?
Both plans give you full access to the library and all of Perlego’s features. The only differences are the price and subscription period: With the annual plan you’ll save around 30% compared to 12 months on the monthly plan.
What is Perlego?
We are an online textbook subscription service, where you can get access to an entire online library for less than the price of a single book per month. With over 1 million books across 1000+ topics, we’ve got you covered! Learn more here.
Do you support text-to-speech?
Look out for the read-aloud symbol on your next book to see if you can listen to it. The read-aloud tool reads text aloud for you, highlighting the text as it is being read. You can pause it, speed it up and slow it down. Learn more here.
Is Dynamic Systems Modelling and Optimal Control an online PDF/ePUB?
Yes, you can access Dynamic Systems Modelling and Optimal Control by Victoria Miroshnik,Dipak Basu in PDF and/or ePUB format, as well as other popular books in Business & Business Strategy. We have over one million books available in our catalogue for you to explore.
Information
1
Optimal Control Problem
Solution of a continuous-time optimal control problem
Pontryagin (1962) and his associates developed the maximum principle for solving continuous-time control problems. Basically, the maximum (or minimum) principle provides a set of local necessary conditions for optimality. According to this method, variables analogous to the Lagrange multipliers should be introduced. These variables, usually denoted by p, are often called the co-state or adjoint-system variables. A scalar-value function H, which generally is a function of x,p,u (state, co-state, control vector) and t, named Hamiltonian function of the problem, is also considered. An economic model can be presented as:
or
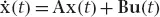
where
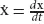
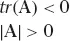
The trajectory of a non-stable system exhibits explosive oscillations. The general solution of the system presented in (1.1) has the form:
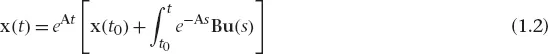
where x(t0) is fixed.
We can rewrite it as (Pontryagin, 1962):
where matrix Φ(t) and the vector r(t) can be computed given t and u(t). Φ(t) is known as the state transition equation or fundamental matrix of solutions.
In an optimal control problem, nominal state and control trajectories, denoted by ẍ(t) and ü(t), are specified, and the performance function to be minimized is:
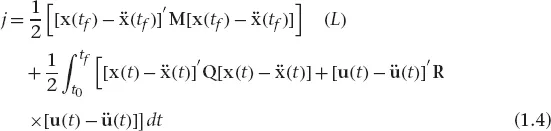
where t0, tf denote the initial and final lime.
Symmetric weighting matrices M,Q and R, are defined as En × En, En × En and Em × Em respectively. Matrix R is assumed to be positive definite whilst the other two may be positive semi-definite.
The control problem is as follows
Minimize the cost function (1.4), with the constraints:
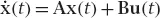
where, x(t0) and t are fixed.
To solve ...