A Pragmatic Guide to Real Options

T. Arnold

• Publisher: Palgrave Macmillan
• Year: 2014
• ISBN:
  9781137391162
• Topic: Business
• Subtopic: Corporate Finance
• Index: Business

Aimed atpractitionerswith no prior expertise in the subject, this bookhelpsreadersbuild basic real options models to aid in decision-making.Providing apragmatic and informative approach, the authorsintroduce basic probability theories, before putting these theories into a real-world context.

C H A P T E R 1

HOW NET PRESENT VALUE IS IMPLEMENTED

WHEN READING CORPORATE FINANCE TEXTBOOKS, NET PRESENT value (NPV) emerges as the preferred metric for project valuation under most circumstances. NPV is intuitively appealing because cash outflows (costs) are being compared to cash inflows to determine if one is bigger than the other. More specifically, all of the cash flows (inflows and outflows) are discounted to generate the NPV calculation: NPV equals the sum of discounted cash inflows less the sum of discounted cash outflows (see the appendix to this chapter for a quick tutorial on discounting).

If the NPV is greater than zero, the firm is overcompensated based on the risk of the project (a good situation). If the NPV is equal to zero, the firm is appropriately compensated based on the risk of the project (an acceptable situation). If the NPV is negative, the firm is undercompensated based on the risk of the project (an unacceptable situation).

A quick example illustrates NPV very readily. Suppose a firm can invest $5,000 (an outflow) to start a project that will generate three years of annual cash flows of $2,000 (inflows). Looking at the undiscounted cash flows, the project appears to be profitable—spend $5,000 to receive $6,000 of total inflows over three years. However, risk needs to be considered relative to these inflows because receipt of the cash flows in the future is not guaranteed.

The consideration of risk is the primary reason for discounting any cash flows that occur in the future. As cash flows become more uncertain, the discount rate increases to adjust for this risk. Generally with an NPV analysis, a discount rate that is constant throughout the life of the project is applied. Assume the discount rate is 10% annually. The sum of the discounted inflows becomes:

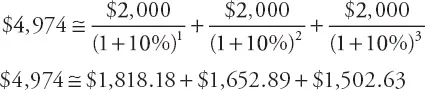
When considering discounted cash flows, the NPV of the project is negative (NPV = $4,974 – $5,000 = –$26; technically, the $5,000 outflow is discounted as well, $5,000 ÷ (1 + 10%)⁰ = $5,000) making the project undesirable despite initially looking profitable when considering undiscounted cash flows.

A related calculation is the project’s internal rate of return (IRR). The IRR is the discount rate that sets the NPV to zero. In the example given earlier, if the discount rate is set to 9.7% annually, the sum of the discounted cash inflows becomes $5,000:

Consequently, 9.7% is the project’s IRR because using 9.7% as the discount rate sets the NPV to zero (i.e., NPV = $5,000 – $5,000 = 0).

By combining the two measures for the project, a possible, but not quite accurate, interpretation of the project is: the riskiness of the project requires a 10% annual return, however, the project can generate only a 9.7% annual return. The negative NPV indicates that the project undercompensates the firm by providing a 9.7% annual return when the risk dictates a 10% annual return as necessary.

If the discount rate was below 9.7% annually, the project would overcompensate the firm for the risk and lead to an NPV greater than zero. Similarly, if the discount rate was 9.7% annually, the project would exactly compensate the firm for the risk and lead to an NPV of zero.

Although overly simplified, the numerical example demonstrates the intuitive interpretation that NPV provides for making decisions about projects. A firm prefers NPVs that are not negative and prefer NPV to be more positive if possible. However, there are some “holes” in the way NPV is applied in this numerical example and in general. To illustrate the problem, consider a bond’s yield to maturity in reference to how a bond is priced.

1.1 THE YIELD TO MATURITY OF A BOND

A bond promises an investor interest in the form of a periodic coupon (assume the coupon is annual for simplicity) with a par payment (the face value of the bond) received when the bond matures. Consider a three-year $1,000 bond with 4% annual coupons. The par value is $1,000 and the annual coupons are $40 (i.e., annual coupon rate multiplied by the par value: 4% × $1,000).

The price of the bond depends on the discounted values of the future inflows of the bond. Because a bond is a debt instrument, one should understand that debt usually has an interest rate that increases with the length of time the debt is outstanding and with the magnitude of the debt. Consequently, the discount rates that apply to the bond should differ based on when the coupon is received, and although received at the same time as the third coupon, the par payment should have a higher interest rate applied because the par payment is many times larger than the coupon payment. Based on these considerations, a credible bond price can be calculated as:

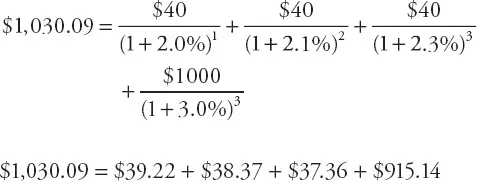
Although meticulous, the calculation of the bond price is very consistent with the idea that the discount rate for the bond’s component parts should differ based on time and magnitude. However, the bond’s yield to maturity is a constant annual discount rate through time applied to the bond’s cash flows to produce the bond price. The yield to maturity for the three-year bond is 2.94% and generates that same price of $1,030.09.

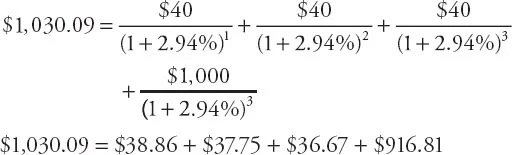
Comparing the two bond prices, the yield to maturity calculation undervalues the coupons and overvalues the par payment to produce an equivalent price. Although not an entirely correct interpretation, the yield to maturity is often viewed as the discount rate for the bond. At best, the yield to maturity is a “summary discount rate” of a more complex app...

Table of contents

• Cover
• Title
• 1  How Net Present Value Is Implemented
• 2  Making Decisions Sequential
• 3  Option Terminology and an Introduction to Binomial Trees
• 4  Binomial Trees, Risk-Neutral Pricing, and American Style Options
• 5  Applying Real Option Analysis with NPV-Embedded Binomial Trees
• 6  Applying More Real Options Analysis into an NPV-Embedded Binomial Tree
• 7  Implementing an NPV-Embedded Binomial Tree from an NPV Analysis
• 8  Real Option Analysis and the Black-Scholes Model
• Index