Equity Derivatives and Hybrids

Markets, Models and Methods

Oliver Brockhaus

• Publisher: Palgrave Macmillan
• Year: 2016
• Print ISBN: 9781137349484
• eBook ISBN: 9781137349491
• Topic: Business
• Subtopic: Business General
• Index: Business

Since the development of the Black-Scholes model, research on equity derivatives has evolved rapidly to the point where it is now difficult to cut through the myriad of literature to find relevant material. Written by a quant with many years of experience in the field this book provides an up-to-date account of equity and equity-hybrid (equity-rates, equity-credit, equity-foreign exchange) derivatives modeling from a practitioner's perspective. The content reflects the requirements of practitioners in financial institutions: Quants will find a survey of state-of-the-art models and guidance on how to efficiently implement them with regards to market data representation, calibration, and sensitivity computation. Traders and structurers will learn about structured products, selection of the most appropriate models, as well as efficient hedging methods while risk managers will better understand market, credit, and model risk and find valuable information on advanced correlation concepts.Equity Derivatives and Hybrids provides exhaustive coverage of both market standard and new approaches, including: -Empirical properties of stock returns including autocorrelation and jumps-Dividend discount models-Non-Markovian and discrete-time volatility processes-Correlation skew modeling via copula as well as local and stochastic correlation factors-Hybrid modeling covering local and stochastic processes for interest rate, hazard rate, and volatility as well as closed form solutions -Credit, debt, and funding valuation adjustment (CVA, DVA, FVA)-Monte Carlo techniques for sensitivities including algorithmic differentiation, path recycling, as well as multilevel.Written in a highly accessible manner with examples, applications, research, and ideas throughout, this book provides a valuable resource for quantitative-minded practitioners and researchers.

1

Empirical Evidence

When studying derivatives it is useful to be aware of the empirical properties of the underlying. Those properties should be taken into account when attempting to model the underlying for the risk management of derivatives. Derivatives often depend on one or more closing prices within a time period ranging from few months up to several years. Thus the focus in this chapter is a time series of closing prices, although the methods can also be applied to higher frequency data.

Let a time series (S_i,i = 0,1,2,…,n) of closing prices for a stock or index be given where i ranges through all business days within a given time interval. Stock returns are defined for i = 1,2,…,n as

As an example consider the European stock index Stoxx 50, Figure 1.1.

The corresponding return sequence in Figure 1.2 shows periods of high volatility in 2002 (dot com bubble) and 2008 (Lehman default).

1.1 Distribution

When analyzing the first four moments of the return distribution one observes that the distribution of returns is negatively skewed (third moment) with heavier tails (fourth moment) than the Gaussian distribution. Figure 1.3 exhibits the empirical density of one business day’s returns from January 1998 to March 2015, in comparison with the Gauss distribution with the same first and second moment. The observed return density motivates Lévy models, including models with as introduced in Section 6.4, as an alternative to the log-normal process of the Black-Scholes model discussed in Section 18.2.

Negative skewness is often explained as being due to risk averse investors in connection with risky stocks. Both news and small negative price movements may trigger larger investors fearing default to cut losses and sell. This effect is not symmetric as investors do not apply the same urgency when reacting to positive price moves. Heavy tails (kurtosis) are a feature of processes with persistent volatility as discussed in Section 1.3.4.

Figure 1.1 Stoxx 50 level

Figure 1.2 Stoxx 50 returns

Figure 1.3 Stoxx 50 density

1.2 Drift

1.2.1 Level

The observed drift level depends on the dividends and interest rate environment. Average returns often exceed the corresponding drift differential of interest rates and dividend yields as shareholders expect to be compensated for taking a higher risk than bond holders. In a risk neutral setting higher drift may also apply. The risk of default or dropping share value due to unpredictable events is compensated for by a drift exceeding the risk free rate. The assumption that equities are a better long term investment than fixed income products has been challenged by repeatedly collapsing equity markets since 2000.

1.2.2 Mean reversion

Equity processes are generally not mean reverting. This assertion can be tested by estimating parameters of the model

using the Augmented Dickey-Fuller test. Vanishing autocorrelation indicates δ = 0. If the null-hypothesis for γ against γ < 0 cannot be rejected then the process does not exhibit mean reversion. Note that mean reversion for an asset is not compatible with the no-arbitrage assumption that in a risk neutral setting the expected return of an asset has to be equal to the risk free interest rate.

1.2.3 Seasonality

Seasonality within equity processes is typically not considered, in contrast to commodities processes. Thus seasonality adjustments via a time-dependent periodic drift function are not made. Periodicity of trading activity and hence volatility can be observed intraday, as well as on a weekly basis and, presumably, to some extent with yearly periodicity. This can be modelled through a trader time function of physical time which grows slower during weekends, holidays and, possibly, closing times of relevant exchanges.

1.3 Autocorrelation

1.3.1 Return level

In order to assess whether returns are independent one can measure the autocorrelation, namely the correlation of R₁,R₂,…,R_n−τ and R_1+τ,R_2+τ,…,R_n. If returns are independent then the outcome should be 1 for τ = 0 and numbers close to 0 for τ > 0. This seems to be supported by the data: the autocorrelation curve labelled ‘returns’ in Figure 1.4 rema...

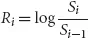
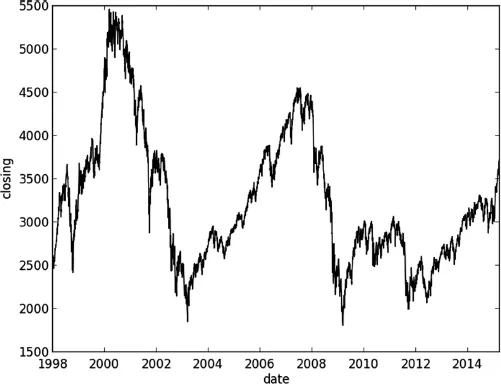
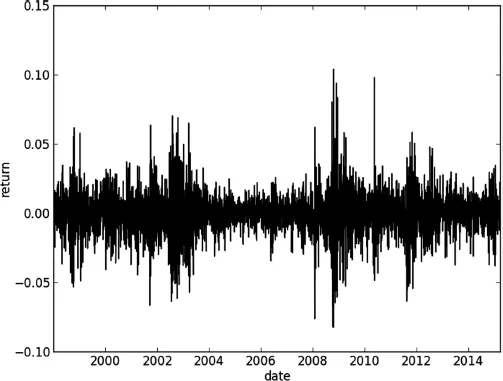
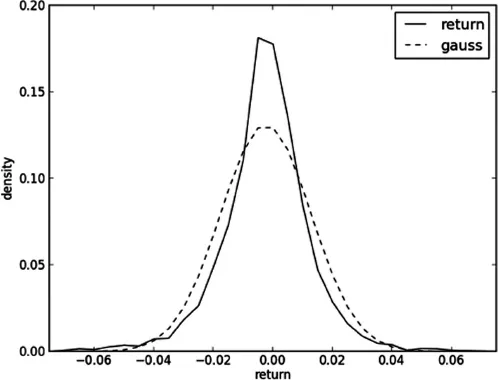
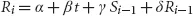
Table of contents

• Cover
• Title Page
• Copyright
• Contents
• List of Figures
• Preface
• Acknowledgements
• List of Notations
• 1 Empirical Evidence
• 2 Equity Derivatives Market
• 3 Exotic Equity Derivatives
• 4 Implied Volatility
• 5 Dividends.
• 6 Short Volatility Models
• 7 Implied Volatility Dynamics
• 8 Correlation
• 9 Copulas
• 10 Fixed Income
• 11 Equity-interest Rate Hybrids
• 12 Credit
• 13 Defaultable Equity
• 14 Counterparty Credit Risk
• 15 Foreign Exchange
• 16 Affine Processes
• 17. Monte Carlo
• 18 Gauss
• References
• Index