Absence of Arbitrage Valuation

A Unified Framework for Pricing Assets and Securities

P. Glabadanidis

• Publisher: Palgrave Macmillan
• Year: 2014
• ISBN:
  9781137372871
• Topic: Business
• Subtopic: Corporate Finance
• Index: Business

Absence of Arbitrage Valuation presents a unified asset pricing strategy through absence of arbitrage and applies this framework to such disparate fields as fixed income security pricing, foreign exchange spots, and forward rates.

1

Asset Pricing Models

1.1 Future Value

Consider investing a current value of V₀ for T periods at the compound periodic rate of r. The future value of the initial investment is given simply by the following:

Note the compounding effect that follows from being able to earn interest in future periods on the interest earned in previous periods. The longer the length of the compounding period T, the more pronounced this effect will be given a fixed starting value V₀ for a fixed r. For a fixed future time period T and initial investment V₀, the compounding effect becomes much more pronounced for larger values of r.

1.2 Present Value

Consider now turning the previous question on its head and ask the following: what is the present value today at t = 0 equal to a given future value of V_T given a periodic opportunity cost of capital equal to r? The answer to this question can be obtained through a simple rearrangement of the future value equation in the previous section as follows:

Note that the further out into the future the cash flow is to be obtained the lower the present value, given a fixed opportunity cost. Similarly, for a fixed future time period T, higher values for the opportunity cost r lead to lower present values today at t = 0.

1.3 Perpetuities

Consider an infinite sequence of cash flows of the same amount C which commences payment at t = 1 and never cease. This is an example of a level payment to be received in perpetuity or, more simply, a perpetuity.

The present value of all of these payments is represented by the following infinite sum:

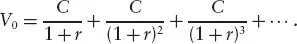
This infinite sum is an example of a geometric series and, provided that r > 0, converges to a finite value

which, after some simplifications of terms in the denominator, is reduced to the following:

Another useful sequence of cash flows is a growing perpetuity. This is very similar to the example just considered where the first cash flow C takes place again at t = 1 and is paid forever, but this time every subsequent payment increases at the rate of g. The present value of this growing perpetuity is given by the infinite sequence:

This is yet another example of an infinite sum of a geometric series which converges to a finite value, provided that g < r, as follows:

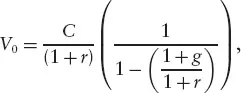
which, after some simplifications, leads to the following:

Note that if g ≥ r, then the present value of the growing perpetuity is infinite. The above formula is only valid for the case where the growth rate is less than r. Applying the formula to a case where g ≥ r is a mistake as witnessed by the resulting negative present value.

1.4 Annuities

Let us now consider a finite stream of cash flows which starts at t = 1 and lasts until t = T > 1 where the same periodic payment C is being paid in every period. The present value of this level annuity is given by

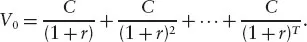
We can evaluate this finite geometric series directly or, alternatively, we realize that the level annuity can be represented as the difference between two perpetuities. The first perpetuity pays off C in every period starting with t = 1, while the second perpetuity pays off C in every period starting with t = T + 1. The difference between the payoffs of these two perpetuities comprises the payoffs of the level annuity. Hence, the present values of the level annuity is the difference between the present values of the two perpetuities:

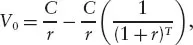
which, after collecting terms, reduces to

Next, let us consider a more general annuity where the period payment increases in every period at the rate of g where the initial payment C takes place again at t = 1 and the last payment is at t = T > 1. The present value of this growing annuity is equal to

We can evaluate this finite sum using the geometric series formula or, alternatively, we can realize that the payoffs of the growing annuity can be repre...

Table of contents

• Cover
• Title
• 1 Asset Pricing Models
• 2 Discounted Cash Flow Valuation
• 3 Relative Valuation with Equity and Value Multiples
• 4 Financial Options
• 5 Real Options
• 6 Fixed Income Securities
• 7 Fixed Income Derivatives
• 8 Foreign Exchange
• 9 What Next?
• Notes
• Bibliography
• Index