
eBook - ePub
Modern Derivatives Pricing and Credit Exposure Analysis
Theory and Practice of CSA and XVA Pricing, Exposure Simulation and Backtesting
- English
- ePUB (mobile friendly)
- Available on iOS & Android
eBook - ePub
Modern Derivatives Pricing and Credit Exposure Analysis
Theory and Practice of CSA and XVA Pricing, Exposure Simulation and Backtesting
About this book
This book provides a comprehensive guide for modern derivatives pricing and credit analysis. Written to provide sound theoretical detail but practical implication, it provides readers with everything they need to know to price modern financial derivatives and analyze the credit exposure of a financial instrument in today's markets.
Frequently asked questions
Yes, you can cancel anytime from the Subscription tab in your account settings on the Perlego website. Your subscription will stay active until the end of your current billing period. Learn how to cancel your subscription.
No, books cannot be downloaded as external files, such as PDFs, for use outside of Perlego. However, you can download books within the Perlego app for offline reading on mobile or tablet. Learn more here.
Perlego offers two plans: Essential and Complete
- Essential is ideal for learners and professionals who enjoy exploring a wide range of subjects. Access the Essential Library with 800,000+ trusted titles and best-sellers across business, personal growth, and the humanities. Includes unlimited reading time and Standard Read Aloud voice.
- Complete: Perfect for advanced learners and researchers needing full, unrestricted access. Unlock 1.4M+ books across hundreds of subjects, including academic and specialized titles. The Complete Plan also includes advanced features like Premium Read Aloud and Research Assistant.
We are an online textbook subscription service, where you can get access to an entire online library for less than the price of a single book per month. With over 1 million books across 1000+ topics, we’ve got you covered! Learn more here.
Look out for the read-aloud symbol on your next book to see if you can listen to it. The read-aloud tool reads text aloud for you, highlighting the text as it is being read. You can pause it, speed it up and slow it down. Learn more here.
Yes! You can use the Perlego app on both iOS or Android devices to read anytime, anywhere — even offline. Perfect for commutes or when you’re on the go.
Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app.
Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app.
Yes, you can access Modern Derivatives Pricing and Credit Exposure Analysis by Roland Lichters,Roland Stamm,Donal Gallagher in PDF and/or ePUB format, as well as other popular books in Économie & Mathématiques d'entreprise. We have over one million books available in our catalogue for you to explore.
Information
I
Discounting
1 |  | Discounting Before the Crisis |
1.1 The risk-free rate
The main ingredient for pricing is the zero curve r(t) which assigns an interest rate to any given maturity t > 0. It tells us what the value of 1 currency unit will be at time t if invested at the risk-free rate. For most theoretical applications, the zero rate is expressed as continuously compounding, so the value at time t will be given by
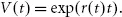
Other conventions are also common. Linear compounding is typically used for short-term interest (less than one year):
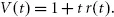
Simple compounding takes interest on interest into account, in particular for maturities beyond one year:
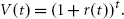
Conversely, today’s value of one currency unit paid in t years is given by
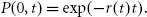
P(0,t) is the price of a risk-free zero bond with maturity t, as seen today (at time 0). It is also referred to as the (deterministic) discount factor for time t, dft.
This immediately raises the question: What is the risk-free rate, which is the compensation to lenders for not using their money for consumption immediately? The person or institution making the promise of paying back the money would have to be seen as non-defaultable, no matter what happens. Obviously, such an entity does not exist, so people use proxies like certain highly rated governments or supra-national institutions. Before the near-default of Bear Stearns, people viewed banks that were rated AA or higher as virtually default-free, and therefore used the LIBOR rate as proxies for the risk-free rate.
1.2 Pricing linear instruments
1.2.1 Forward rate agreements
The most important building block in interest rate modelling is the forward rate agreement, or FRA for short. This is a contract by which two parties agree today (at t = 0) on an interest rate f(0;t1,t2) to be paid in t2 for a loan spanning a future period t1 to t2. If the market (i.e. LIBOR) rate L(t1,t2) which is fixed in t1 for that period exceeds f(0;t1,t2), the payer of the rate has made a profit. Otherwise, the receiver gains more than the market rate.
Market practice is that the payment is actually paid in t1 by computing the cash flow in t2 and discounting it to t1 with the fixed LIBOR rate. For pricing purposes, this is virtually irrelevant (see [117]), so we ignore this distinction.
Pricing this correctly is obviously equivalent to predicting the LIBOR rate in a market-accepted manner.
What rate can we expect in three months’ time if we want to borrow money for six months at that time? Calculate the forward rate of a 3M into 9M FRA as follows:
• Borrow df0.25 = P(0,0.25) units for three months at the risk-free three-month rate
• Invest the money for nine months at the risk-free rate for nine months
• Borrow 1 unit in an FRA in three months (maturing six months later) to pay back the loan with interest
• After another six months, pay back the loan with the df0.25/df0.75 from the investment
• By the no-arbitrage principle, the combination has to be worth 0. The forward rate therefore has to be
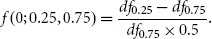
Note that, in general, the period lengths are not exactly a quarter or half a year but rather depend on the day count fraction of the rates used. In Euroland, this would be ACT/360, for example.
In Figure 1.1, we must have (assuming linear compounding, as is the market custom for periods of less than one year)
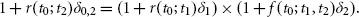
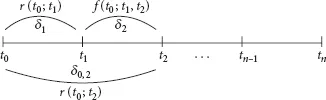
Figure 1.1 Replication of the forward rate
In other words
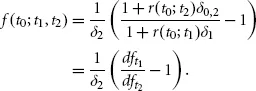
In general, the forward rate for time t (in years from today) for a period of δ (in years) is given by
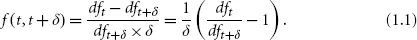
The present value of the forward rate paid on a notional of 1 unit is therefore
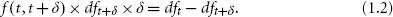
Note that this is true because we use the same discount factors in the forward rate replication as when discounting cash flows. The main assumption in this replication argument is that I (at least a bank) can borrow and lend arbitrary amounts at the risk-free (LIBOR) rate.
We can take a look at what happens if we let δ approach 0 in formula (1.1), under the assumption that the discount curve is differentiable:
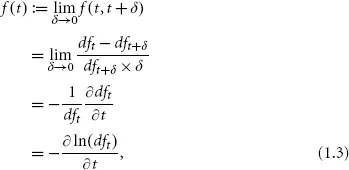
which also implies that
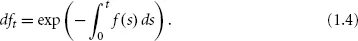
Forward rates are used as expected values for the LIBOR fixing for a future time period. Most importantly, this is done in interest rate swaps.
1.2.2 Interest rate swaps
An interest rate swap, or swap for short, is a contract by which two parties agree to exchange interest payments on a predetermined notional on a regular basis. One party pays the fixed rate with the frequency which is standard in the chosen currency. For EUR, for instance, this is annually; for USD, on the other hand, this is semi-annually. The other party pays a floating rate linked to LIBOR of some given frequency (1, 3, 6 or 12 months), possibly with a spread. There is also a standard frequency for floating legs in most currencies: in EUR, this is six months, and in USD, it is three months, for instance.
At inception, the v...
Table of contents
- Cover
- Title Page
- Copyright
- Contents
- List of Figures
- List of Tables
- Preface
- Acknowledgements
- List of Abbreviations and Symbols
- Part I: Discounting
- Part II: Credit and Debit Value Adjustment
- Part III: Risk Factor Evolution
- Part IV: XVA
- Part V: Credit Risk
- Part VI: Appendix
- Bibliography
- Index