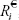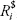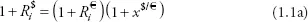Applied International Finance II, Second Edition

Thomas O'Brien

• Publisher: Business Expert Press
• Year: 2017
• Print ISBN: 9781631579226
• eBook ISBN: 9781631579233
• Topic: Business
• Subtopic: Finance
• Index: Business

This volume is the second of a three-volume set designed for use in a course in applied international corporate finance for managers and executives. This volume's issue is how uncertain foreign exchange (FX) rate changes affect a firm's ongoing cash flows and equity value, and what can be done in terms of hedging this risk using financial instruments. The accounting implications are also considered. Numerous examples of real-world companies are used. The volume contains a hypothetical case that ties the material together. The first volume reviews some basics of FX rates: Introduction to Foreign Exchange Rates, 2nd edition, Business Expert Press, 2016. The third volume deals with the estimation of the cost of capital for international operations and the evaluation of overseas investment proposals: Applied International Finance II: International Cost of Capital and Capital Budgeting, 2nd edition, Business Expert Press, 2017.

CHAPTER 1

Global Risk and Return

As the future value of an investment is usually uncertain, an investor needs to think in terms of an expected rate of return. The investor has a target expected rate of return that will compensate for the risk specific to the investment. That target expected rate of return is sometimes called the required rate of return for the investment. Given the risk taken, an investor makes a sound investment if the actual expected rate of return exceeds the required rate of return.

Finance models are often cast in terms of an investment’s aggregate required rate of return, meaning the “market’s” required rate of return. This is sometimes called the opportunity cost of capital, or simply the investment’s cost of capital. Another synonym is the equilibrium expected rate of return, which is the expected rate of return only if the investment is correctly priced in the market.

An important question is which risk–return model is best to use to determine how an investment’s cost of capital should be traded off against the investment’s risk. A long-standing risk–return model is the traditional Capital Asset Pricing Model (CAPM), which is covered in many finance courses and used extensively by practitioners.

In this chapter and the next, we extend the CAPM to internationally integrated financial markets. Given the significant extent of real-world financial market integration and international diversification, an international risk–return model seems logically superior to the traditional CAPM, which is usually applied as a local (or domestic) risk–return model.

This chapter introduces the simple global CAPM (GCAPM), which looks like the traditional CAPM except that the global market index replaces the domestic market index. The international CAPM (ICAPM) is more complex but theoretically stronger than the GCAPM. The next chapter introduces a version of the ICAPM that has some benefits that may justify the additional complexity.

In some currencies, including the US dollar, the simpler GCAPM provides an acceptable approximation to the more complex ICAPM estimate of an asset’s cost of capital. However, the GCAPM may not give an acceptable approximation to the ICAPM when estimating cost of capital in some other currencies or when estimating currency risk premiums.

Traditional CAPM Review

The traditional CAPM is a widely used risk–return model: In a 2012 survey of 19 highly regarded U.S. companies, all but one reported using the CAPM to estimate cost of capital. The CAPM continues to be controversial in academic circles, but remains the primary risk–return model in finance textbooks. A 2009 survey of finance professors found that 75% recommend the CAPM approach to the cost of capital.¹

The well-known traditional CAPM equation is k_i = r_f + β_i[MRP], where k_i is asset i’s cost of capital; r_f is the risk-free rate of return; β_i is asset i’s risk measure (called “beta”); and MRP denotes the market risk premium, which is the risk premium required on the market index by the representative investor. We next elaborate on all four of these variables.

The k_i variable is also called asset i’s equilibrium expected rate of return, which is only equal to the actual expected asset return if the asset is correctly priced in the market.

A standard practice in U.S. applications has been to use a U.S. Treasury yield for r_f. Historically, there has been disagreement on whether to use a short-term or long-term rate. Recent survey evidence shows that managers strongly prefer using a long-term rate.²

The “beta” risk measure, β_i, is asset i’s sensitivity to unexpected returns on the market index. If an asset has a beta of 1.20 and the market index’s rate of return is 10% higher than expected, then the asset’s rate of return will tend to be (on average) 1.20(10%) = 12% higher than expected. The beta of the market index is 1, by definition.

The market risk premium, MRP, is equal to k_M − r_f, which is the required rate of return on the market index minus the risk-free rate; k_M − r_f is the compensation for the risk in the diversified portfolio represented by the market index, and is properly named the MRP. As with individual assets, the difference between the market index’s actual expected rate of return and the risk-free rate is not truly a risk premium because the market index’s possible misvaluation is incorporated.

In the traditional CAPM, the market price of risk is the MRP divided by the variance of market index returns, where the variance measures aggregate market risk. The market price of risk is driven by the average investor’s degree of risk aversion. Thus, the MRP tends to change as overall market volatility changes and as investors’ tolerance for risk fluctuates with economic conditions.

Years ago, it was standard to use a range of 7% to 9% for the U.S. MRP. More recent estimates for the U.S. MRP tend to be in the range of 4% to 7%.³ Exhibit 1.1 shows some U.S. market risk premium estimates over recent years, which are from Aswath Damodaran’s website. The average of the MRP estimates is 5.65%.

Given the modern range of 4% to 7%, reasonable estimates of the U.S. MRP are: In a “normal” market period, use an estimate in the 5% to 6% range. If the market is relatively depressed due to heightened risk aversion (“fear”), use an MRP estimate in the 6% to 7% range. And if the market is in an aggressive stage with higher tolerance for risk (“greed”), use an estimate in the 4% to 5% range.

Exhibit 1.1 U.S. market risk premium (MRP) estimates

2002	4.73%
2003	4.74%
2004	4.86%
2005	5.22%
2006	6.12%
2007	4.59%
2008	6.92%
2009	4.64%
2010	6.09%
2011	8.34%
2012	7.30%
2013	4.99%
2014	5.38%
2015	5.16%

Source: Damodaran: http://pages.stern.nyu.edu/~adamodar/

Rate of Return on a Foreign Asset

We first address the notion of a given asset’s rate of return in different currencies. Specifically, an asset’s rate of return in one currency depends on the rate of return in another currency and the change in the spot FX rate between the two currencies, as shown in equation (1.1a). Equation (1.1a) shows the conversion of asset i’s rate of return in euros,

, to the same asset’s rate of return in US dollars,

, using the percentage change in the FX price of the euro (in US dollars), x^$/€.

Asset’s Rate of Return in Different Currencies

For example, if an asset’s rate of return in euros is 20%, and the euro appreciates by 5% versus the US dollar, the same asset’s rate of return in US dollars is (1.20)(1.05) − 1 = 0.26, or 26%.

The rate of return in British pounds on a share of stock on the London Stock Exchange is 15%. During the same period, the British pound depreciates by 8% versus the US dollar. Find the rate of return on the stock from the US dollar perspective.

Answer: (1.15)(1 − 0.08) − 1 = 0.058, or 5.8%.

A NASDAQ stock’s rate o...

Table of contents

• Cover
• Half-title Page
• Title Page
• Copyright
• Contents
• Acknowledgments
• Review of Foreign Exchange Rates
• Chapter 1 Global Risk and Return
• Chapter 2 The International CAPM
• Chapter 3 Hurdle Rates for Overseas Operations
• Chapter 4 Converting Hurdle Rates and Expected Cash Flows Across Currencies
• Chapter 5 Cross-Border Valuation
• Chapter 6 International Capital Budgeting Applications
• Case Study: New Plant for Houston Marine Electronics
• Notes
• Bibliography
• Index
• Backcover