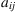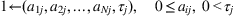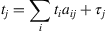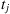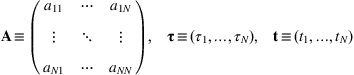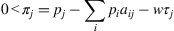Return of Marxian Macro-dynamics in East Asia

Masao Ishikura, Seongjin Jeong, Minqi Li, Masao Ishikura, Seongjin Jeong, Minqi Li, Masao Ishikura, Seongin Jeong, Minqi Li

• Publisher: Emerald Publishing Limited
• Year: 2017
• Print ISBN: 9781787144781
• eBook ISBN: 9781787149410
• Topic: Economics
• Subtopic: Political Economy
• Index: Economics

The economic growth in East Asia has been believed to be the model case of the triumph of capitalism. Some progressive economists, for example, the developmental state theorists, also praised the East Asian model as the progressive alternative to neoliberal market fundamentalism, arguing that they are the outcomes of state-led development. 

However, with the sudden advent of the 'Lost Decade of Japan' in the 1990s, and the ensuing 'IMF Crisis' of South Korea in 1997, and now the imminent 'hard landing' of the Chinese economy, the East Asian miracle story is quickly becoming a thing of the past. East Asia has now become an epicentre of the contradictions and crisis of global capitalism. Today, deepening economic crises, exacerbation of social polarization, rising popular discontents, and escalating geopolitical tensions are common to China, Japan and Korea. Moreover, East Asia has been at the centre of global ecological contradictions. Indeed, East Asia has now become the typical place of Marxian macro-dynamics. ;

This important and timely volume brings together experts in political economy from across the globe, to comment on the return of Marxian macro-dynamics in East Asia. The contributions explore macro-dynamics, the role of the state and hegemony in the context of transnational capitalism, and Marxian alternatives for East Asia.

PART I
MACRO-DYNAMICS IN EAST ASIA

LABOR VALUE AND EXPLOITATION IN THE GLOBAL ECONOMY

Taiji Hagiwara

ABSTRACT

This paper discusses labor value and the rate of exploitation in the global economy using international input–output tables. Labor value is defined as the multiplication of the labor coefficient and Leontief inverse. Exploitation means that the amount of labor embodied in the received wage commodity is less than the amount of the labor actually sold. Therefore, the Fundamental Marxian Theorem, which states that the conditions for the existence of profit and those for the existence of exploitation are the same, should be modified to stipulate that the existence of profit requires exploitation in at least one country. In other words, exploitation may not exist in some countries (non-exploitation). In the context of international input–output tables, we introduce the concept of global labor value, which is the vector of embodied labor in various countries. In the empirical study using an international input–output table, we find that (1) there are non-exploitation cases in several countries. (2) During the time period 1995–2009, the rate of exploitation increased in Asian countries, namely China, Japan, Korea, and Taiwan, whereas the advanced countries other than Asia faced a decreased rate of exploitation.

Keywords: Exploitation; global economy; input–output tables; Fundamental Marxian Theorem; labor value

INTRODUCTION

In classical economics, including Marx, labor value was considered as a good proxy for price. Since the marginal revolution, economists have explained prices as being determined by demand and supply, and the concept of labor value was thought to be obsolete. But Marx found a more important role for labor value as a good tool to explain the existence of exploitation. He insisted that the existence of profit is conditioned by the existence of exploitation.

According to Marx, labor value is the sum of living labor and dead labor. While the notion of living labor is obvious, that of dead labor is arguable. Dead labor is the value of constant capital which is circulation capital (intermediate input) and fixed capital. However, measuring the value of a commodity requires a value for constant capital. Okishio (1955) formulated this as labor value in his system of equations, using the input–output framework developed by Leontief (1941) which he then proved mathematically. Later, Morishima (1973) named this the Fundamental Marxian Theorem.

Among numerous discussions on the Theorem, two points receive the maximum attention. The first point is joint production which means that multiple outputs are produced in single production activity. However, many cases of joint production except fixed capital seem to have less importance in the real economy. Fixed capital, in turn, can be treated in a more simplified way.

The second point is heterogeneity of labor. There are various kinds of jobs, whose skill levels vary. However, if not unified as simple labor, the Theorem may not hold. Okishio (1965) showed how various labor types can be unified by incorporating training labor. Bowles and Gintis (1977) took another approach and proved that although some types of labor may not be exploited, at least one kind of labor must be exploited in order for profit to exist under a heterogeneous labor situation. This paper aims to expand on this approach by using international input–output (IO) tables to determine the existence of non-exploited labor in several Asian countries.

Various empirical studies have used input–output tables, for example, Okishio (1958), Gupta and Steedman (1971), Nakatani (1976), Ochoa (1989), Nakajima and Izumi(1995), Fröhlich (2012), and so on. Some compromises are required when using these tables in an empirical study. One important compromise is international trade. Until the 1980s, only single-country IO tables existed. In a single-country IO table, economic transactions are not closed within the country. The labor value of import commodities must be defined. Okishio (1958) assumed that this equals the labor value of export commodities, for which the monetary value is the same as that of imports.

When international input–output tables were first planned, Katano (1984) tried to formulate labor value in the international IO framework but this attempt was incomplete. Nakatani and Hagiwara (in Nakatani, 1994) defined global labor value and expanded the Fundamental Marxian Theorem as heterogeneous labor value (Bowles & Gintis, 1977). Hagiwara (2004) examined global labor using Japan-USA-Asia-Europe international IO tables 1985–1990 and found that the labor value of Japan’s laborers’ wage commodity basket is larger than their working hours. Following this approach of using international IO tables to measure labor value across countries, this paper uses IO tables to investigate the presence of non-exploited labor in several Asian countries.

LABOR VALUE AND EXPLOITATION IN A SINGLE ECONOMY

Labor value is defined as the labor embodied in one commodity. In the commodity’s production process, labor is incorporated as direct labor. In addition, the commodity is used as intermediate input or fixed capital. Intermediate input and fixed capital are also, in turn, products of labor, intermediate input and fixed capital, and so on. Although such calculations may seem to go back indefinitely, labor value is solved in a system of equations.

Labor Value in a Single Economy

Suppose there are N commodities. Each commodity needs some commodity and labor inputs. That is,

units of commodity¹ i and

units of labor are required to produce one unit commodity j

Labor value, t, is defined as

Labor value

represents the total labor inputs needed to produce commodity j and may therefore be considered the labor embodied in commodity j. In the matrix form,

where

Its solution is

where I_N represents an N × N identity matrix. Since the reciprocal of labor value shows the amount of product produced by a unit of labor either directly or indirectly,

can be called labor productivity. In the context of input–output analysis, labor value can be called an employment multiplier. Labor value

is positive if the matrix

satisfies the Hawkins–Simon condition.²

Conditions for Profit’s Existence in a Single Economy

Profit in each sector should be positive.

where p_j is the output price of sector j, and w is the nominal wage rate. In matrix form,

...

Table of contents

• Cover
• Title Page
• Introduction: Return of Marxian Macro-Dynamics in East Asia
• Part I Macro-Dynamics in East Asia
• Part II State and Hegemony in East Asia in the Context Of Transnational Capitalism
• Part III Consideration of Aspects for a Marxian Alternative for East Asia
• Part IV Communications on Chapters on Sraffa in RPE
• Index