Algebra: Polynomials, Galois Theory and Applications

Frédéric Butin

• Publisher: Dover Publications
• Year: 2017
• Print ISBN: 9780486810157
• eBook ISBN: 9780486818849
• Topic: Mathematics
• Subtopic: Abstract Algebra
• Index: Mathematics

Suitable for advanced undergraduates and graduate students in mathematics and computer science, this precise, self-contained treatment of Galois theory features detailed proofs and complete solutions to exercises. Originally published in French as Algèbre — Polynômes, théorie de Galois et applications informatiques, this 2017 Dover Aurora edition marks the volume's first English-language publication.
The three-part treatment begins by providing the essential introduction to Galois theory. The second part is devoted to the algebraic, normal, and separable Galois extensions that constitute the center of the theory and examines abelian, cyclic, cyclotomic, and radical extensions. This section enables readers to acquire a comprehensive understanding of the Galois group of a polynomial. The third part deals with applications of Galois theory, including excellent discussions of several important real-world applications of these ideas, including cryptography and error-control coding theory. Symbolic computation via the Maple computer algebra system is incorporated throughout the text (though other software of symbolic computation could be used as well), along with a large number of very interesting exercises with full solutions.

PART II

Galois theory

CHAPTER 3

---

Algebraic extensions

---

In this chapter, we define algebraic extensions, which are the preliminary tools for studying Galois theory.

3.1 Algebraic extensions

Let K be a field. An extension of K is a field L whose K is a subfield.

Let K be a field, L be an extension of K, and P ∈ K[X] be a polynomial of degree n. One says that P splits over L if P possesses n roots in L.

A sequence of extensions of the form K₁ ⊂ K₂ ⊂ ··· ⊂ K_n is sometimes called a tower of fields.

3.1.1 Algebraic elements

Proposition 3.1.1

Let K be a field and P ∈ K[X] be a nonconstant polynomial. Then there exists an extension L of K over which P splits.

Proof:

We proceed by induction on the degree n of P.

— The proposition is obvious for a polynomial of degree 1.

— Let us assume that the proposition is true for degree n — 1, and let us prove it for degree n. Let Q be an irreducible factor of P in K[X]. Then L := K[X] / (Q) is a field. Since the map

from K to L is a field homomorphism, it is injective, so that K can be identified with a subfield of L. Let

be the image of X by this homomorphism. Then

, thus x is a root of Q, hence of P in L. In this way, there exists R ∈ L[X] such that P = (X – x)R. We have ∂°(R) = ∂°(P) – 1, thus by the induction hypothesis, there exists an extension L′ of L over which R splits. Then P splits over L′.

Let B be a ring and A be a subring of B. For every x ∈ B, the associated evaluation homomorphism is the map

from A[X] to B. Its image is the smallest subring of B containing A and x, i.e., the ring A[x] of polynomials in x with coefficients in A. For the kernel of e_x, we distinguish two cases:

— Either Ker(e_x) = {0}: x does not satisfy any nontrivial algebraic relation. One says that x is transcendental over A.

— Or Ker(e_x) is nontrivial, i.e., x is a root of a nonzero polynomial with coefficients in A. Then one says that x is algebraic over A.

If B is a field, we ...

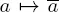
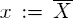
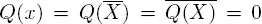
Table of contents

• Cover
• Title Page
• Copyright Page
• Preface
• Introduction
• Contents
• I Arithmetic, rings and polynomials
• II Galois theory
• III Applications
• Biography of quoted mathematicians
• Index
• References
• About the Author