Nonlinear Programming

An Introduction

Peter Zörnig

• Publisher: De Gruyter
• Year: 2014
• Print ISBN:
  9783110315271
• eBook ISBN:
  9783110372519
• Topic: Mathematics
• Subtopic: Mathematical Analysis
• Index: Mathematics

This book is an introduction to nonlinear programming. It deals with the theoretical foundations and solution methods, beginning with the classical procedures and reaching up to "modern" methods like trust region methods or procedures for nonlinear and global optimization. A comprehensive bibliography including diverse web sites with information about nonlinear programming, in particular software, is presented. Without sacrificing the necessary mathematical rigor, excessive formalisms are avoided. Several examples, exercises with detailed solutions, and applications are provided, making the text adequate for individual studies.

The book is written for students from the fields of applied mathematics, engineering, economy, and computation.

1 Introduction

1.1 The model

Many problems of operations research, engineering and diverse other quantitative areas maybe formulated as an optimization problem. Basically, such a problem consists of maximizing or minimizing a function of one or several variables such that the variables satisfy certain constraints in the form of equations or inequalities.

Let us consider the following standard form of an optimization problem:

min ƒ(x)

subject to

(1.1)

where ƒ : ℝⁿ → ℝ, g_i : ℝⁿ → ℝ(i = 1,..., m, see the Notations at the beginning of the book) are real-valued functions of n variables. In this book we will restrict ourselves to the case in which all these functions are continuous. We are searching for a point

such that

0 for i = 1,..., m and

for all x satisfying the inequalities in (1.1).

An example for (1.1) with n = 3 and m = 2 is the problem

subject to

In this case we have

. (Note that ƒ(x) consists of the total expression following the symbol “min”.)

Instead of (1.1) we may use one of the compact forms:

min ƒ(x)

subject to

(1.2)

with M := {x ∈ ℝⁿ |g_i(x) ≤ 0; i = 1,...,m} or

min ƒ(x)

subject to

(1.3)

where g₁(x) := (g₁(x),...,g_m (x))^T is a vector-valued function and 0 is the null vector of ℝ^m.

The function ƒ will be called the objective function, and the inequalities in (1.1) are called constraints or restrictions. The elements of the set M in (1.2) are called feasible solutions or feasible points and M is referred to as a feasible set or feasible region. A point

∈ M is called an optimal solution or optimal point of (1.1) if

holds for all x ∈ M. The value

of an optimal solution

is called the optimal value. Whenever we refer to “the solution” of an optimization problem, an optimal solution is meant.

Various optimization problems, which are not written in the form (1.1) can be reformulated as a problem in standard form. For example, in the case of maximization we can transform

(1.4)

into the equivalent problem

(1.5)

Of course, the optimal values of (1.4) and (1.5) differ in sign. An inequality g_i (x) ≥ 0 can be written as – g_i (x) ≤ 0, and the equation g_i(x) = 0 can be substituted by the two inequalities

We emphasize that in practice equ...

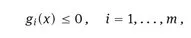
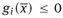
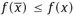
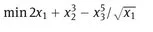
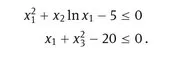
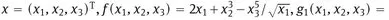
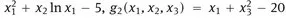
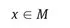
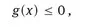
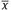
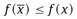
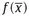
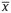
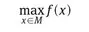
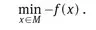
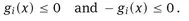
Table of contents

• Title Page
• Copyright Page
• Preface
• Table of Contents
• Notations
• 1 Introduction
• Part I: Theoretical foundations
• Part II: Solution methods
• Appendix: Solutions of exercises
• References
• Index