Elements of Partial Differential Equations

Pavel Drábek, Gabriela Holubová

• Publisher: De Gruyter
• Year: 2014
• Topic: Mathematics
• eBook ISBN:
  9783110374049
• Subtopic: Applied Mathematics
• Index: Mathematics

This textbook is an elementary introduction to the basic principles of partial differential equations. With many illustrations it introduces PDEs on an elementary level, enabling the reader to understand what partial differential equations are, where they come from and how they can be solved. The intention is that the reader understands the basic principles which are valid for particular types of PDEs, and to acquire some classical methods to solve them, thus the authors restrict their considerations to fundamental types of equations and basic methods. Only basic facts from calculus and linear ordinary differential equations of first and second order are needed as a prerequisite.

The book is addressed to students who intend to specialize in mathematics as well as to students of physics, engineering, and economics.

Chapter 1

Motivation, Derivation of Basic Mathematical Models

The beginning and development of the theory of partial differential equations were connected with physical sciences and with the effort to describe some physical processes and phenomena in the language of mathematics as precisely (and simply) as possible. With the invasion of new branches of science, this mathematical tool found its usage also outside physics. The width and complexity of problems studied gave rise to a new branch called mathematical modeling. The theory of partial differential equations was set apart as a separate scientific discipline. However, studying partial differential equations still stays closely connected with the description – modeling – of physical or other phenomena.

In this introductory chapter, we outline the derivation of several basic mathematical models, which we will deal with in more detail in the further text.

1.1 Conservation Laws

In our text, the notion of a mathematical model is understood as a mathematical problem whose solution describes the behavior of the studied system. In general, a mathematical model is a simplified mathematical description of a real-world problem. In our case, we will deal with models described by partial differential equations, that is, differential equations with two or more independent variables.

Studying natural, technical, economical, biological, chemical and even social processes, we observe two main tendencies: the tendency to achieve a certain balance between causes and consequences, or the tendency to break this balance. Thus, as a starting point for the derivation of many mathematical models, we usually use some law or principle that expresses such a balance between the so called state quantities and flow quantities and their spatial and time changes.

Let us consider a medium (body, liquid, gas, solid substance, etc.) that fills a domain

Here N denotes the spatial dimension. In real situations, usually, N = 3, in simplified models, N = 2 or N = 1. We denote by

the state function (scalar, vector or tensor) of the substance considered at a point x and time t. In further considerations, we assume u to be a scalar function. The flow function (vector function, in general) of the same substance will be denoted by

The density of sources at a point x and time t is usually described by a scalar function

Let Ω_B ⊂ Ω be an arbitrary inner subdomain (the so called balance domain) of Ω. The integral

represents the total amount of the considered quantity u in the balance domain Ω_B at time t. The integral

then represents the total amount of the quantity in Ω_B and in the time interval [t₁, t₂ ] ⊂ [0, T). (The set Ω_B x [t₁, t₂ ] is called the space-time balance domain.)

In particular, if the state function u(x, t) corresponds to the mass density ϱ(x, t), then the integral

represents the mass of the substance in the balan...

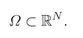
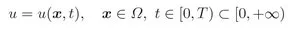
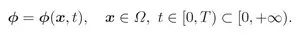
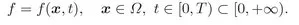
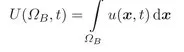
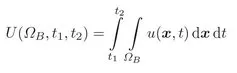
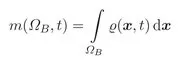
Table of contents

• Title Page
• Copyright Page
• Preface
• Table of Contents
• Chapter 1 - Motivation, Derivation of Basic Mathematical Models
• Chapter 2 - Classification, Types of Equations, Boundary and Initial Conditions
• Chapter 3 - Linear Partial Differential Equations of the First Order
• Chapter 4 - Wave Equation in One Spatial Variable –Cauchy Problem in ℝ
• Chapter 5 - Diffusion Equation in One Spatial Variable –Cauchy Problem in ℝ
• Chapter 6 - Laplace and Poisson Equations in Two Dimensions
• Chapter 7 - Solutions of Initial Boundary Value Problems for Evolution Equations
• Chapter 8 - Solutions of Boundary Value Problems for Stationary Equations
• Chapter 9 - Methods of Integral Transforms
• Chapter 10 - General Principles
• Chapter 11 - Laplace and Poisson equations in Higher Dimensions
• Chapter 12 - Diffusion Equation in Higher Dimensions
• Chapter 13 - Wave Equation in Higher Dimensions
• Appendix A - Sturm-Liouville Problem
• Appendix B - Bessel Functions
• Some Typical Problems Considered in this Book
• Bibliography
• Index