Convex Analysis and Optimization in Hadamard Spaces

Miroslav Bacak

• Publisher: De Gruyter
• Year: 2014
• Print ISBN: 9783110361032
• eBook ISBN: 9783110391084
• Edition: 1
• Topic: Mathematics
• Subtopic: Functional Analysis
• Index: Mathematics

In the past two decades, convex analysis and optimization have been developed in Hadamard spaces. This book represents a first attempt to give a systematic account on the subject.

Hadamard spaces are complete geodesic spaces of nonpositive curvature. They include Hilbert spaces, Hadamard manifolds, Euclidean buildings and many other important spaces. While the role of Hadamard spaces in geometry and geometric group theory has been studied for a long time, first analytical results appeared as late as in the 1990s. Remarkably, it turns out that Hadamard spaces are appropriate for the theory of convex sets and convex functions outside of linear spaces. Since convexity underpins a large number of results in the geometry of Hadamard spaces, we believe that its systematic study is of substantial interest. Optimization methods then address various computational issues and provide us with approximation algorithms which may be useful in sciences and engineering. We present a detailed description of such an application to computational phylogenetics.

The book is primarily aimed at both graduate students and researchers in analysis and optimization, but it is accessible to advanced undergraduate students as well.

1 Geometry of nonpositive curvature

The first chapter is devoted to basic notions in metric spaces including a geodesic, metric midpoint and an angle. We define geodesic metric spaces and then explain how one can compare geodesic triangles in these spaces with triangles in the Euclidean plane. Such comparisons enable us to define nonpositive curvature in geodesic spaces and hence to define Hadamard spaces. The condition of nonpositive curvature can be neatly expressed by an analytical inequality and, since we are concerned more with analysis than geometry, this is how we shall use it in our developments. We however feel it is also helpful to gain a geometrical intuition for Hadamard spaces and therefore we start with the triangle comparisons. The chapter ends by providing a number of equivalent conditions for Hadamard spaces.

Unless stated otherwise, the 2-dimensional vector space ℝ² is assumed to be equipped with the Euclidean norm

The corresponding inner product is denoted 〈·,·〉.

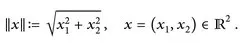
1.1 Geodesic metric spaces

Let (X, d) be a metric space. A continuous mapping from the interval [0, 1] to X is called a path. The length of a path γ: [0, 1] → X is defined as

where the supremum is taken over the set of all partitions 0 = t₀ < ... < t_n = 1 of the interval [0, 1], with an arbitrary

. Given a pair of points x, γ ∈ X, we say that a path y: [0,1] → X joins x and y if γ(0) = ϰ and γ(1) = y. A metric space (X, d) is a length space if for every x, γ ∈ X and ε > 0 there exists a path γ: [0, 1] → X joining x and γ such that length(γ) ≤ d(x, γ) + ε. If γ: [0, 1] → X is a path and t ∈ [0, 1], we often use the symbol γ_t to denote the point γ(t).

A path γ: [0, 1] → X is called a geodesic if d(γ_s, γ_t) = d(γ₀, γ₁)|s — t| for every s, t ∈ [0, 1], that is, if it parametrized proportionally to the arc length. In particular, a geodesic is an injection unless it is trivial, that is, unless γ₀ = γ₁. When no confusion is likely, we do not distinguish between a geodesic γ: [0, 1] → X an...

Table of contents

• De Gruyter Series in Nonlinear Analysis and Applications
• Title Page
• Copyright Page
• Preface
• Table of Contents
• 1 Geometry of nonpositive curvature
• 2 Convex sets and convex functions
• 3 Weak convergence in Hadamard spaces
• 4 Nonexpansive mappings
• 5 Gradient flow of a convex functional
• 6 Convex optimization algorithms
• 7 Probabilistic tools in Hadamard spaces
• 8 Tree space and its applications
• References
• Index
• De Gruyter Series in Nonlinear Analysis and Applications