Nonlinear Dynamics

Mathematical Models for Rigid Bodies with a Liquid

Ivan A. Lukovsky, Peter V. Malyshev

• Publisher: De Gruyter
• Year: 2015
• eBook ISBN: 9783110389739
• Edition: 1
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

This book is devoted to analytically approximate methods in the nonlinear dynamics of a rigid body with cavities (containers) partly filled by a liquid. The methods are normally based on the Bateman-Luke variational formalism combined with perturbation theory. The derived approximate equations of spatial motions of the body-liquid mechanical system (these equations are called mathematical models in the title) take the form of a finite-dimensional system of nonlinear ordinary differential equations coupling quasi-velocities of the rigid body motions and generalized coordinates responsible for displacements of the natural sloshing modes. Algorithms for computing the hydrodynamic coefficients in the approximate mathematical models are proposed. Numerical values of these coefficients are listed for some tank shapes and liquid fillings. The mathematical models are also derived for the contained liquid characterized by the Newton-type dissipation. Formulas for hydrodynamic force and moment are derived in terms of the solid body quasi-velocities and the sloshing-related generalized coordinates. For prescribed harmonic excitations of upright circular (annular) cylindrical and/or conical tanks, the steady-state sloshing regimes are theoretically classified; the results are compared with known experimental data.

The book can be useful for both experienced and early-stage mechanicians, applied mathematicians and engineers interested in (semi-)analytical approaches to the "fluid-structure" interaction problems, their fundamental mathematical background as well as in modeling the dynamics of complex mechanical systems containing a rigid tank partly filled by a liquid.

Chapter 1

Governing equations and boundary conditions in the dynamics of a bounded volume of liquid

1.1 Conservation laws. Governing equations

The motion of continua is most frequently described by using two approaches developed by Lagrange and Euler. The Lagrange approach is based on the use of the basic theorems of mechanics for the direct description of every individual liquid particle by tracking its position with the help of a function of time, whereas the Euler equations deal with the distribution of the velocity field in the analyzed liquid domain. In what follows, we consider, following Euler, the velocity field with components υ_x, υ_y, and υ_z as functions of the space variables and time. Then the trajectories of individual particles can be obtained by the integration of the system of ordinary differential equations ẋ = υ_x, ẏ = υ_y , ż = υ_z, where the dots over x, y, and z denote the operation differentiation with respect to the time preformed along the motion of an individual particle.

We now present some auxiliary formulas frequently used in what follows to deduce the equations of motion and for some other purposes. It is important to be able to perform the mathematical operation of evaluation of the time derivatives of various hydrodynamical quantities related to a given liquid particle in the course of its motion.

Let A(x, y, z, t) be a hydrodynamic quantity related to a particle moving along the trajectory x = x(t), y = y(t), z = z(t). By definition, the quantity

is the velocity vector related to the particle. For this particle, the variables x, y,z of the function A(x, y, z, t) are also functions of t and characterize the motion of the particle. According to the rule of differentiation of a composite function, we get

(1.1.1)

This formula for the total derivative can also be represented in the form

(1.1.2)

Another frequently used formula related to the hydrodynamic quantity A(x, y, z, t) is the time derivative of the expression J = ∫_τ Adτ, where τ is a time-dependent liquid domain containing the same particles for the entire period of motion.

The value of the integral J varies in the course of time due to the variations of the integrand A and the liquid domain τ. For two close times, we get the following formula:

(1.1.3)

Here,

is an element of the domain τ − τ′. To within the terms of higher orders in Δt, we obtain

where S is the surface of τ and υ_ν is the external normal velocit...

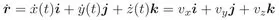
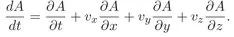
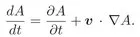
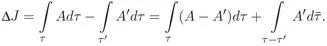
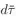
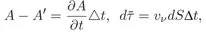
Table of contents

• De Gruyter Studies in Mathematical Physics 27
• Titel
• Impressum
• Foreword to English Edition
• Foreword to Russian Edition
• Inhaltsverzeichnis
• Introduction
• Chapter 1 - Governing equations and boundary conditions in the dynamics of a bounded volume of liquid
• Chapter 2 - Direct methods in the nonlinear problems of the dynamics of bodies containing liquids
• Chapter 3 - Hydrodynamic theory of motions of the ships transporting liquids
• Chapter 4 - Nonlinear differential equations of space motions of a rigid body containing an upright cylindrical cavity partially filled with liquid
• Chapter 5 - Nonlinear modal equations for noncylindical axisymmetric tanks
• Chapter 6 - Derivation of the nonlinear equations of space motions of the body–liquid system by the method of perturbation theory
• Chapter 7 - Equivalent mechanical systems in the dynamics of a rigid body with liquid
• Chapter 8 - Forced finite-amplitude liquid sloshing in moving vessels
• Bibliography
• Index
• De Gruyter Studies in Mathematical Physics