Concepts of Proof in Mathematics, Philosophy, and Computer Science

Dieter Probst, Peter Schuster, Dieter Probst, Peter Schuster

• Publisher: De Gruyter
• Year: 2016
• Print ISBN: 9781501510809
• eBook ISBN: 9781501502644
• Edition: 1
• Topic: Philosophy
• Subtopic: History & Philosophy of Mathematics

A proof is a successful demonstration that a conclusion necessarily follows by logical reasoning from axioms which are considered evident for the given context and agreed upon by the community. It is this concept that sets mathematics apart from other disciplines and distinguishes it as the prototype of a deductive science. Proofs thus are utterly relevant for research, teaching and communication in mathematics and of particular interest for the philosophy of mathematics. In computer science, moreover, proofs have proved to be a rich source for already certified algorithms.

This book provides the reader with a collection of articles covering relevant current research topics circled around the concept 'proof'. It tries to give due consideration to the depth and breadth of the subject by discussing its philosophical and methodological aspects, addressing foundational issues induced by Hilbert's Programme and the benefits of the arising formal notions of proof, without neglecting reasoning in natural language proofs and applications in computer science such as program extraction.

Ulrik Buchholtz . Gerhard Jäger , and Thomas Strahm

Theories of Proof-Theoretic Strength ψ(ΓΩ+1)

Ulrik Buchholtz: Department of Philosophy, Carnegie Mellon University, Pittsburgh, PA 15213-3890, USA, e-mail: [email protected]

Gerhard Jäger and Thomas Strahm: Institut für Informatik, Universität Bern, Neubrückstrasse 10, 3012 Bern, Switzerland, e-mail: {jaeger,strahm}@iam.unibe.ch

Abstract: The purpose of this article is to present a range of theories with proof-theoretic ordinal ψ(ΓΩ+1). This ordinal parallels the ordinal of predicative analysis, Γ0, and our theories are parallel to classical theories of strength Γ0 such as

, and .

We also relate these theories to the unfolding of ID1 which was already presented in the PhD thesis of the first author as a system of strength ψ(ΓΩ+1)

Keywords: Subsystems of second order arithmetic and inductive definitions, Proof-theoretic ordinals, Unfolding

Mathematics Subject Classification 2010: 03F03, 03F05, 03F015, 03F35

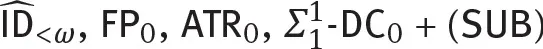
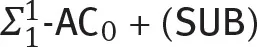
1Introduction

The ordinal ψ(ΓΩ+1) appeared first in [Bachmann, 1950], there it is denoted by

.19This was the paper where Bachmann introduced the idea of using assigned fundamental sequences to ordinals of the third number class in order to define large countable ordinals, and this is what Howard [Howard, 1972] uses in his original ordinal analysis of ID1. ID1 is the theory of one generalized positive inductive definition, and its proof-theoretic ordinal is now known as the Bachmann-Howard ordinal.

Miller [Miller, 1976] proposed that ψ(ΓΩ+1) should be the proof-theoretic ordinal of a theory that relates to ID1 as predicative analysis r...

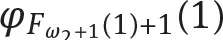
Table of contents

• Cover
• Title Page
• Copyright
• Preface
• Contents
• Introduction
• Herbrand Confluence for First-Order Proofs with Π2-Cuts
• Proof-Oriented Categorical Semantics
• Logic for Gray-code Computation
• The Continuum Hypothesis Implies Excluded Middle
• Theories of Proof-Theoretic Strength ψ(ΓΩ+1)
• Some Remarks about Normal Rings
• On Sets of Premises
• Non-Deterministic Inductive Definitions and Fullness
• Cyclic Proofs for Linear Temporal Logic
• Craig Interpolation via Hypersequents
• A General View on Normal Form Theorems for Łukasiewicz Logic with Product
• Relating Quotient Completions via Categorical Logic
• Some Historical, Philosophical and Methodological Remarks on Proof in Mathematics
• Cut Elimination in Sequent Calculi with Implicit Contraction, with a Conjecture on the Origin of Gentzen’s Altitude Line Construction
• Hilbert’s Programme and Ordinal Analysis
• Aristotle’s Deductive Logic: a Proof-Theoretical Study
• Remarks on Barr’s Theorem: Proofs in Geometric Theories
• Endnotes