Phononic Crystals

Vincent Laude

• Publisher: De Gruyter
• Year: 2015
• ISBN:
  9783110387919
• Edition: 1
• Topic: Physical Sciences
• Subtopic: Waves & Wave Mechanics

Phononic crystals are artificial periodic structures that can alter efficiently the flow of sound, acoustic waves, or elastic waves. They were introduced about twenty years ago and have gained increasing interest since then, both because of their amazing physical properties and because of their potential applications. The topic of phononic crystals stands as the cross-road of physics (condensed matter physics, wave propagation in inhomogeneous and periodic media) and engineering (acoustics, ultrasonics, mechanical engineering, electrical engineering). Phononic crystals cover a wide range of scales, from meter-size periodic structures for sound in air to nanometer-size structures for information processing or thermal phonon control in integrated circuits. Phononic crystals have a definite relation with the topic of photonic crystals in optics. The marriage of phononic and photonic crystals also provides a promising structural basis for enhanced sound and light interaction.

As the topic is getting popular, it is nowadays presented and discussed at various international conferences. After the first ten years during which the topic has remained mainly theoretical with a few proof-of-concept demonstrations in the literature, the evolution has been towards applications, instrumentation, and novel designs. The physical explanations for various effects are now well understood and efficient numerical methods and analysis tools have been developed.

The book contains a comprehensive set of finite element model (FEM) scripts for solving basic phononic crystal problems. The scripts are short, easy to read, and efficient, allowing the reader to generate for him(her)self band structures for 2D and 3D phononic crystals, to compute Bloch waves, waveguide and cavity modes, and more.

1 Introduction

Phononic crystals were officially born in 1993 after a famous paper by Kushwaha and co-authors [74] drawing the analogy to acoustic waves of the photonic crystal concept for light, which itself had been inspired by the theory of electrons in crystal lattices. Of course this statement is a simplification, and deciding that phononic crystals were born at a certain time is just putting a name on an idea that was ready to start living its own life as it detached from the tree of the physics of waves in periodic media. Over the last twenty years, the phononic concept has developed gracefully. It has been researched by many authors and has reached maturity in the sense that it became ready to be the subject of a monograph. The purpose of this book is to propose a selfcontained presentation of the topic, going from the basics of the physics of waves upto the description of potential applications.

Preliminary comments. The topic of phononic crystals is clearly a branch of physical acoustics, and even more so a branch of the physics of waves. For completeness, in Chapter 2 we have gathered a synthetic presentation of many concepts of wave propagation in periodic media. The material in that chapter is elementary and independent from the concepts and the specific equations of physical acoustics. The presentation is limited to scalar waves, but introduces some important and fruitful tools such as Bloch’s theorem, the band structure, evanescent waves, basic mechanisms for band gap formation, the classification of artificial crystals according to their Bravais lattices, and primitive cells and the first Brillouin zone. All these are used abundantly in the subsequent chapters.

The materials inside which waves will be considered to propagate can be broadly classified as either fluids (liquids, gases) or solids (natural crystals, amorphous solids, metals, piezoelectric solids, etc.). A note on terminology is needed here. Although the physical concepts are globally shared, the wave equations in fluids and solids differ mathematically. We will speak of acoustic waves as the pressure waves propagating in fluids; they can be described by a time-dependent scalar field in three-dimensional space, which we denote p(t, x). In Chapter 3 we have gathered a self-consistent presentation of linear acoustic waves in fluids, including water and air. In the case of solids, elastic waves are described most conveniently by a vector field of particle displacements, which we denote u(t, x). The implication is that elastic waves have a polarization and that even homogeneous solids can be naturally anisotropic, including the important case of natural crystals. We shall try to reserve the adjective “acoustic” for pressure waves, but the practice in the literature is very often to use it for elastic waves in solids as well. Chapter 5 summarizes the topic of elastic waves in homogeneous solids, introducing such important concepts as anisotropy, piezoelectricity, surface elastic waves, and plate waves.

As the material in Chapters 2, 3, and 5 is not specific to phononic crystals, those chapters may be skipped by the knowledgeable reader. Please note, however, that frequent or implicit reference is made to their contents in the other chapters.

Artificial crystals. By artificial crystals we mean periodic material systems that were made by technology or craft. The adjective artificial is used to differentiate them from natural crystals, which are the topic of solid state physics and are the support of phonons – the particles of sound in matter. Artificial crystals usually have a periodicity measured by a length, the lattice constant, that is much larger than the interatomic distances in natural crystals. For this reason they can be treated macroscopically using the equations of continuum mechanics. Still elastic waves in solids can be considered as the asymptotic limit of acoustic phonons, which is a reason for the choice of the name “phononic crystal”.

Fig. 1.1: Artificial crystals for waves in 1D, 2D, and 3D. The crystals depicted are composed of a periodic repetition of a certain distribution of solid or fluid matter, or possibly voids. The smallest volume that can be used to pave all space by periodicity is a primitive cell of the crystal. Material distribution is implicitly assumed to be continuous within the different regions but discontinuous at their interfaces.

The phononic crystal appeared around 1993, as we said earlier, and is an artificial crystal for elastic waves in solids. It is typically composed of a periodic alternation of at least two different materials, or a periodic heterostructure, as depicted in Figure 1.1 Depending on the number of periodicities, we shall classify them as one-dimensional (1D), two-dimensional (2D), or three-dimensional (3D) phononic crystals. Of course, it is perfectly possible to consider in theory phononic crystals defined from continuous variations of elastic parameters (mass density and elastic constants), but practical realizations almost always involve discontinuous regions of different materials. It is also perfectly possible to replace one material with holes, as the surface boundary conditions at the surface of the holes will provide the necessary scattering properties. As a note for readers interested in photonic crystals, a vacuum does not support elastic wave propagation, in contrast to optical waves in free space; this is a major difference between phononic and photonic crystals. Another difference is the polarization of elastic waves, which admit three independent modes of propagation in general, whereas there are two independent optical modes of propagation in dielectric materials. Phononic crystals are first introduced in Chapter 6.

Sonic crystals are artificial crystals for pressure waves in fluids. In the literature, the terms phononic crystal and sonic crystal are often used indifferently to encompass all cases of artificial crystals for mechanical waves. For clarity, we shall generally imply more restrictive and separate meanings: sonic crystals for acoustic or pressure waves, and phononic crystals for elastic waves. Sonic crystals are first introduced in Chapter 4 and support only one mode of propagation. They can be composed of a periodic distribution of different fluids, like air bubbles in water, but true voids or holes will not be permitted in practice. By extension, the very common case of solid inclusions in a fluid matrix will also be referred to as a sonic crystal. Indeed, although all three propagation modes of elastic waves exist in the solid inclusions, measurements of the properties of fluid-solid crystals are made via pressure waves. For exactly the inverse reason, fluid inclusions in a solid matrix will be termed a phononic crystal. Coupling of elastic and acoustic waves, and some associated effects, are discussed in Chapter 8.

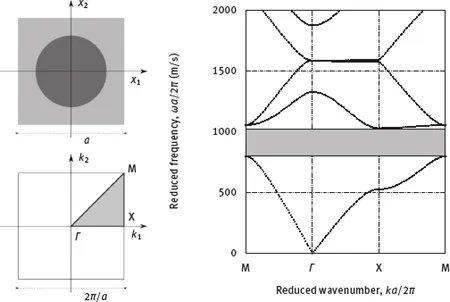
As artificial crystals, sonic and phononic crystals owe a lot to condensed matter physics and borrow concepts that have been used to describe electronic and photonic band structures, as well as phonons in crystal lattices. The concept of Bloch waves – the natural modes of periodic media – is ubiquitous. Their dispersion properties are presented in diagrams called band structures, plotted with reference to first Brillouin zones, as Chapter 2 explains. Maybe the most salient property of artificial crystals is the existence of band gaps, or frequency ranges inside which propagating Bloch waves are absent whatever the wavenumber and thus propagation is not allowed. A partial band gap is valid for at least one direction in k-space, but not necessarily for others. A complete band gap is valid for all values of the wavevector k, that is for any direction of propagation, but possibly for only one polarization mode. A full band gap is a complete band gap that is valid for all polarization modes and thus for all possible waves in the crystal. The distinction between full and complete band gaps is only meaningful for phononic crystals, both definitions being equivalent for sonic crystals. As a note, the distinction between full and complete band gap is not generally made in the literature, but we shall try to stick to it in this book for clarity. As an example, Figure 1.2 displays the band structure of a 2D square-lattice sonic crystal of steel rods in water, together with the corresponding first Brillouin zone. The diameter of the rods has been chosen such that a complete – or full in this case – band gap appears.

Mechanisms for band gap formation. It is perfectly possible to go a long way with sonic and phononic crystals with just numerical simulations, solving the acoustic or elastodynamic equations to obtain Bloch waves and to plot phononic band structures, or computing the transmission through a finite crystal to locate frequency band gaps. Beyond numerical computation, however, an important question is the physical origin for the opening of a band gap. The most common and the historically first invoked physical mechanism is Bragg interference. Bragg scattering occurs at every periodic plane of scatterers inside a crystal. Bragg band gaps can be created anytime a forward and a backward propagating Bloch wave are phase matched, i.e. when they would have degenerated in the band structure space (k, ω) if they did not couple. In the limit of a vanishingly small material contrast, such band crossings occur in the empty lattice model at every high symmetry point of the first Brillouin zone. This is the phenomenological reason why Bragg band gaps appear at symmetry points in reciprocal space, and hence along the irreducible Brillouin zone. In Figure 1.2, band foldings occur at points Γ, X, and M of the first Brillouin zone. The author however humbly recognizes he does not know of a mathematical demonstration of this property in the general case of medium or strong material contrast.

Fig. 1.2: Band structure example for a 2D square-lattice sonic crystal. The sonic crystal is composed of cylindrical steel rods in water. The ratio of the rod diameter to the lattice constant a is 0.83. The first Brillouin zone is sketched at the bottom left. For the square lattice, the first Brillouin zone is also a square whose high symmetry points are noted Γ, X, and M. The irreducible first Brillouin zone is further defined with respect to all symmetries of the unit cell and shaded in gray. The band structure on the right shows the dispersion of propagating Bloch waves as the relation between wavenumber k and angular frequency ω. It is plotted along the boundary of the irreducible first Brillouin zone as path [Γ-X-M-Γ]. The area shaded in gray in the band structure indicates a complete – or full, in the sonic crystal case, – band gap.

A second possible physical mechanism for band gap formation is the existence of a local resonance in the internals of the unit cell of the crystal [89]. In this case, there is possibility for part of the incoming wave energy to be trapped for some time in the resonator before it is radiated away to all permitted propagation modes. The local resonance principle is discussed in Chapter 10 and can be viewed as a classical analog of the Fano resonance, i.e. as the coupling of a continuum of propagating waves with a localized resonant state.

There are quite different types of phononic crystals that have been considered in the literature. On the one hand, when inspired by photonic crystals, or because of technological constraints when going to the microscale, the inclusions in the unit cell are quite often limited to simple shapes such as cylinders or spheres. In such conditions the possible geometries are rather limited and the engineering efforts to design artificial crystals are mostly directed to material constant contrast. On the other hand, when the lattice constant is not too small, there may be enough room for structural design with small-scale details inside the unit cell. Both types of phononic crystals, based on material contrast or structural design, can sustain the two mechanisms of band gap formation we discussed above.

Whenever a band gap is present, it is traditional to say that no wave can propagate through the crystal. Though this statement is perfectly correct, it says nothing about the other waves that can exist at frequencies within a band gap range. Band gaps are actually the realm of evanescent Bloch waves. Evanescent waves are plane waves whose wavenumber is complex valued. The imaginary part of the wavenumber is especially significant as it describes the exponential decay or amplification of the evanescent wave. The transmission through a finite length crystal at frequencies within a band gap range is governed by exponentially decaying evanescent waves. Evanescent Bloch waves and the complex band structure are introduced in Chapter 9.

Applications of phononic crystals. The potential applications of phononic and sonic crystals cover the full range of microsonics, ultrasonics, and audible frequencies. At the small scale, when the lattice constant is of the order of one micron, phononic crystals can be combined with surface acoustic wave technology (SAW), thin-film bulk acoustic resonators, and with microelectromechanical systems (MEMS). Chapter 7 introduces the fundamentals of surface and Lamb wave phononic crystals.

Full band gaps, when they exist, in principle offer a very convenient platform for designing functionalities such as mirrors, cavities, and waveguides. Indeed, adding a defect in an otherwise perfectly periodic crystal is a powerful way to localize the flow of acoustic or elastic energy. This idea is exemplified in many different instances in Chapter 11.

Sonic and phononic crystals are strongly dispersive, meaning that the conditions for propagation of waves can change drastically with only small changes in the frequency. The effects of spatial and temporal dispersion, the exploitation of crystal anisotropy to achieve positive or negative refraction, and the variations of the group velocity are discussed in Chapter 12.

This book is also about numerical simulation. One very strong motivation during the writing of the book was to offer the reader a rather complete knowledge to perform numerical simulations in most situations that occur with sonic and phononic crystal. Overall, the book can also be viewed as a practical guide to numerical simulation of sonic and phononic crystals, especially with the finite element method (FEM) and in view of obtaining Bloch waves and band structures. There is also a presentation of using FEM methods to solve problems in acoustic wave propagation and scattering, and in elastic wave propagation in bulk anisotropic and piezoelectric media, at surfaces, and in plates. The choice was made to insist on some simple variational formulations that describe the physics of wave propagation while leaving the technical details of mathematical solving to an FEM code and the technical details of domain meshing to specialized software. The examples in the book have been obtained with the open source FEM software FreeFem++ [48]. Meshing of 3D unit cells was performed with the open source software gmsh [41]. A full explanation of the plane wave expansion (PWE) method is also provided, with full consideration of anisotropic materials and piezoelectricity.

This book is not about . . . some possibly important topics! The extent of every subject has to be bounded by some arbitrary choices. Some topics that have a close connection to phononic crystals have not been included in our presentation, such as acoustic metamaterials, wave propagation in periodic structures of applied mechanics, structural optimization of phononic crystals, thermal phonon control, phoxonic crystals and optomechanics. A short introduction to some of these topics is given in the general conclusion.

Part I: Acoustic waves in sonic crystals

Tout estoit sans beauté, sans reglement, sans flamm...