
- 247 pages
- English
- ePUB (mobile friendly)
- Available on iOS & Android
About this book
Written for mathematicians working with the theory of graph spectra, this (primarily theoretical) book presents relevant results considering the spectral properties of regular graphs. The book begins with a short introduction including necessary terminology and notation. The author then proceeds with basic properties, specific subclasses of regular graphs (like distance-regular graphs, strongly regular graphs, various designs or expanders) and determining particular regular graphs. Each chapter contains detailed proofs, discussions, comparisons, examples, exercises and also indicates possible applications. Finally, the author also includes some conjectures and open problems to promote further research.
Contents
Spectral properties
Particular types of regular graph
Determinations of regular graphs
Expanders
Distance matrix of regular graphs
Frequently asked questions
- Essential is ideal for learners and professionals who enjoy exploring a wide range of subjects. Access the Essential Library with 800,000+ trusted titles and best-sellers across business, personal growth, and the humanities. Includes unlimited reading time and Standard Read Aloud voice.
- Complete: Perfect for advanced learners and researchers needing full, unrestricted access. Unlock 1.4M+ books across hundreds of subjects, including academic and specialized titles. The Complete Plan also includes advanced features like Premium Read Aloud and Research Assistant.
Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app.
Information
1Introduction
1.1Terminology and notation
Vertices and edges
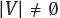
Table of contents
- Cover
- Titelseite
- Impressum
- Preface
- Inhalt
- List of Figures
- 1 Introduction
- 2 Spectral properties
- 3 Particular types of regular graph
- 4 Determinations of regular graphs
- 5 Expanders
- 6 Distance matrix of regular graphs
- References
- Graph index
- Index