Absolutely Small

Michael D. Fayer

• Publisher: AMACOM
• Year: 2010
• eBook ISBN: 9780814414910
• Topic: Physical Sciences
• Subtopic: Quantum Theory

Absolutely Small presents (and demystifies) the world of quantum science like no book before.

Physics is a complex, daunting topic, but it is also deeply satisfying?even thrilling. When liberated from its mathematical underpinnings, physics suddenly becomes accessible to anyone with the curiosity and imagination to explore its beauty. Science without math? It's not that unusual.

For example, we can understand the concept of gravity without solving a single equation. So for all those who may have pondered what makes blueberries blue and strawberries red; for those who have wondered if sound really travels in waves; and why light behaves so differently from any other phenomenon in the universe, it's all a matter of quantum physics.

This book explores in considerable depth scientific concepts using examples from everyday life, such as:

• particles of light,
• probability,
• states of matter,
• what makes greenhouse gases bad

Challenging without being intimidating, accessible but not condescending, Absolutely Small develops your intuition for the very nature of things at their most basic and intriguing levels.

1
Schrödinger’s Cat

WHY ARE CHERRIES RED and blueberries blue? What is the meaning of size? These two questions seem to be totally unrelated. But, in fact, the second question doesn’t seem to be a question at all. Don’t we all know the meaning of size? Some things are big, and some things are small. But, the development of quantum theory showed that the first two questions are intimately related and that we had a completely false concept of size until a couple of decades into the twentieth century. Our ideas about size, if we thought about size at all, worked just fine in our everyday lives. But beginning in approximately 1900, the physics that was used to describe all of nature, and the physics that still works remarkably well for landing a spacecraft on Mars, began to fall apart. In the end, a fundamentally new understanding of size was required not only to explain why cherries are red and blueberries are blue, but also to understand the molecules that make up our bodies, the microelectronics that run our computers, why carbon dioxide is a greenhouse gas, and how electricity can move through metals. Our everyday experiences teach us to think in terms of classical physics, the physics that was greatly advanced and formalized by Sir Isaac Newton (1642–1727). Everything we know from early childhood prepares us to view nature in a manner that is fundamentally wrong. This book is about the concept of absolute size and its consequence, quantum theory, which requires us to fundamentally change our way of thinking about nature. The first half of the book describes the basic concepts of quantum theory. The second half applies quantum theory to many aspects of the world around us through an examination of the properties of atoms and molecules and their roles in everyday life.

This book began with a simple question. Does quantum mechanics make sense? I was asked to address this question at “Wonderfest 2005, the Bay Area Festival of Science,” sponsored by the University of California at Berkeley Department of Physics and the Stanford University Department of Chemistry. Wonderfest is a yearly event that presents a variety of lectures on “the latest findings” in a number of fields to an audience of nonspecialists. However, I was not asked to discuss the latest findings in my own research, but the topic, “does quantum mechanics make sense,” which has been argued about by scientists and laypeople alike since the inception of quantum theory in 1900. In addition, I had only one-half hour to present my affirmative answer to the question. This was a tall order, so I spent several months thinking about the subject and a great deal of time preparing the lecture. After the event, I thought I had failed—not because it is impossible to make plain the important issues for nonspecialists, but because the time constraint was so severe. To get to the crux of the matter, certain concepts must be introduced so that contrasts between classical mechanics and quantum mechanics can be drawn. This book is my opportunity to address the quantum theory description of nature with sufficient time to do the subject justice. The book uses very simple math involving at most small equations. The idea is to make quantum theory completely accessible to the nonscientist. However, the fact that the book requires essentially no math does not mean that the material is simple. Reading Kierkegaard requires no math but is not simple. However, unlike Kierkegaard, the meaning of the material presented below should be evident to the reader who is willing to do a little mental exercise.

Classical mechanics describes the motion of a baseball, the spinning of a top, and the flight of an airplane. Quantum mechanics describes the motion of electrons and the shapes of molecules such as trans fats, as well as electrical conductivity and superconductivity. Classical mechanics is a limiting case of quantum mechanics. Quantum mechanics contains classical mechanics but not vice versa. In that respect, classical mechanics is wrong. However, we use classical mechanics to design bridges, cars, airplanes, and dams. We never worry about the fact that the designs were not done using the more general description of nature embodied in quantum theory. The use of classical mechanics will not cause the bridges to collapse, the cars to crash, the airplanes to fall from the sky, or the dams to burst. In its own realm, the realm of mechanics that we encounter in everyday life, classical mechanics works perfectly. Our intuitive feel of how the world works is built up from everyday experiences, and those experiences are, by and large, classical. Nonetheless, even in everyday life classical mechanics cannot explain why the molecules in a blueberry make it blue and the molecules in a cherry make it red. The instincts we have built up over a lifetime of observing certain aspects of nature leave us unprepared to intuitively understand other aspects of nature, even though such aspects of nature also pervade everyday life.

SCHRÖDINGER’S CAT

Schrödinger’s Cat is frequently used to illustrate the paradoxes that seem to permeate the quantum mechanical description of nature. Erwin Schrödinger (1887–1961) and Paul A.M. Dirac (1902–1984) shared the Nobel Prize in Physics in 1933 for their contributions to the development of quantum theory, specifically “for the discovery of new productive forms of atomic theory.” Schrödinger never liked the fundamental interpretation of the mathematics that underpins quantum theory. The ideas that bothered Schrödinger are the exact topics that will be discussed in this book. He used what has come to be known as “Schrödinger’s Cat” to illustrate some of the issues that troubled him. Here, Schrödinger’s Cat will be reprised in a modified version that provides a simple illustration of the fact that quantum mechanics doesn’t seem to make sense when discussed in terms of everyday life. The cats offered here are to drive the issues home and are not in Schrödinger’s original form, which was more esoteric. The scenario presented will be returned to later. It will be discussed as an analogy to real experiments explained by quantum theory, but not as an actual physical example of quantum mechanics in action.

Imagine that you are presented with 1000 boxes and that you are going to participate in an experiment by opening them all. You are told that there is a half-dead cat in each box. Thus, if you opened one of the boxes, you might expect to find a very sick cat. Actually, the statement needs to be clarified. The correct statement is that each of the cats is not half dead, but rather each cat is in a state that is simultaneously completely dead and perfectly healthy. It is a 50-50 mixture of dead and healthy. In other words, there is a 50% chance that it is dead and a 50% chance that it is alive. Each of the thousand cats in the thousand boxes is in the exact same state. The quantum experimentalist who prepared the boxes did not place 500 dead cats in 500 boxes and 500 live cats in the other 500 boxes. Rather, he placed identical cats that are in some sense 50-50 mixtures of dead and perfectly healthy in each box. While the cats are in the closed boxes, they do not change; they remain in the live-dead mixed state. Furthermore, you are told that when you open a box and look in, you will determine the cat’s fate. The act of looking to see if the cat is alive will determine if the cat is dead or alive.

You open the first box, and you find a perfectly healthy cat. You open the next three boxes and find three dead cats. You open another box and find a live cat. When you are finished opening the 1000 boxes, you have found 500 live cats and 500 dead cats. Perhaps, more astonishing, would be if you start again with a new set of one 1000 boxes, each containing again a 50-50 mixture of live-dead cats. If you open the boxes in the same order as in the first trial, you will not necessarily get the same result for any one box. Say box 10 in the first run produced a live cat on inspection. In the second run, you may find it produced a dead cat. The first experimental run gives you no information on what any one box will contain the second time. However, after opening all 1000 boxes on the second run, you again find 500 live cats and 500 dead cats.

I have to admit to simplifying a little bit here. In two runs of the Schrödinger’s Cats experiment, you probably would not get exactly 500 live and 500 dead cats on each run. This is somewhat like flipping an honest coin 1000 times. Because the probability of getting heads is one half and the probability of getting tails is one half, after 1000 flips you will get approximately 500 heads. However, you might also get 496 heads or 512 heads. The probability of getting exactly 500 heads or 500 live cats out of 1000 trials is 0.025 (2.5%). The probability of getting 496 heads is 0.024 (2.4%) and 512 heads is 0.019 (1.9%). The probability of getting only 400 heads or 400 live cats out of 1000 trials is 4.6 × 10^–11 = 0.000000000046. So the probable outcomes are clustered around 500 out of a 1000 or 50%. Knowing that you have 1000 Schrödinger’s Cat boxes with 50-50 mixtures of live-dead cats or 1000 flips of an honest coin, you can’t say what will happen when you open one box or flip the coin one time. In fact, you can’t even say exactly what will happen when you open all 1000 boxes or flip the coin 1000 times. You can say what the probability of getting a particular result is for one event and what the likely cumulative results will be for many events.

NOT LIKE FLIPPING COINS

A fundamental difference exists between Schrödinger’s Cats, or more correctly real quantum experiments, and flipping pennies. Before I flip a penny, it is either heads or tails. When I flip it, I may not know what the outcome will be, but the penny starts in a well-defined state, either heads or tails, and ends in a well-defined state, either heads or tails. It is possible to construct a machine that flips a penny so precisely that it always lands with the same result. Nothing inherent in nature prevents the construction of such a machine. If a penny with heads up is inserted into the machine, a switch could determine whether the penny lands heads or tails. In flipping a coin by hand, the nonreproducibility of the flip is what randomizes the outcome. However, a box containing Schrödinger’s Cat is completely different. The cat is a 50-50 mixture of live and dead. It is the act of opening the box and observing the state of the cat that causes it to change from a “mixed state” into a “pure state” of either alive or dead. It doesn’t matter how precisely the boxes are opened. Unlike flipping pennies, a machine constructed to open each of the 1000 boxes exactly the same way will not make the results come out the same. The only thing that can be known about opening any one box is that there is a 50% chance of finding a live cat.

REAL PHENOMENA CAN BEHAVE LIKE SCHRÖDINGER’S CATS

As described, the Schrödinger’s Cat problem cannot be actualized. However, in nature many particles and situations do behave in a manner analogous to opening Schrödinger’s Cat boxes. Particles such as photons (particles of light), electrons, atoms, and molecules have “mixed states” that become “pure states” upon observation, in a manner like that described for Schrödinger’s Cats. The things that make up everyday matter, processes, and phenomena behave at a fundamental level in a way that, at first, is as counterintuitive as Schrödinger’s Cats. However, the problem does not lie with the behavior of electrons and atoms, but rather with our intuition of how things should behave. Our intuition is based on our everyday experiences. We take in information with our senses, which are only capable of observing phenomena that involve the behavior of matter governed by the laws of classical mechanics. It is necessary to develop a new understanding of nature and a new intuition to understand and accept the quantum mechanical world that is all around us but not intuitively understandable from our sensory perceptions.

2
Size Is Absolute

THE FUNDAMENTAL NATURE OF SIZE is central to understanding the differences between the aspects of the everyday world that fit into our intuitive view of nature and the world of quantum phenomena, which is also manifested all around us. We have a good feel for the motion of baseballs, but we mainly gloss over our lack of knowledge of what gives things different colors or why the heating element in an electric stove gets hot and glows red. The motion of baseballs can be described with classical mechanics, but color and electrical heating are quantum phenomena. The differences between classical and quantum phenomena depend on the definition of size.

The quantum mechanical concept of size is the correct view, and it is different from our familiar notion of size. Our common concept of size is central to classical mechanics. The failure to treat size properly, and all of the associated consequences of that failure, is ultimately responsible for the inability of classical mechanics to properly describe and explain the behavior of the basic constituents of matter. A quantum mechanical description of matter is at the heart of technological fields as diverse as microelectronics and the computer design of pharmaceuticals.

SIZE IS RELATIVE IN EVERYDAY LIFE

In classical mechanics, size is relative. In quantum mechanics, size is absolute. What does relative versus absolute size mean, and why does it matter?

In classical mechanics and in everyday life, we determine whether something is big or small by comparing it to something else. Figure 2.1 shows two rocks. Looking at them, we would say that the rock on the left is bigger than the rock on the right. However, because there is nothing else to compare them to, we can’t tell if they are what we might commonly call a big rock and a small rock. Figure 2.2 shows the rock on the left again, but this time there is something to compare it to. The size of the rock is clear because we have the size of a human hand as a reference. Because we know how big a typical hand is, we get a good feel for how big the rock is relative to the hand. Once we have the something against which to make a size comparison, we can say that the rock is relatively small, but not tiny. If I were to describe the rock over the phone, I could say it is somewhat bigger than the palm of your hand, and the person I am talking to would have a good idea of how big the rock is. In the absence of something of known size for comparison, there is no way to make a size determination.

FIGURE 2.1. Two rocks.

Figure 2.1 demonstrates how much we rely on comparing one thing to another to determine size. In Figure 2.1, the two rocks are on a white background, with no other features for reference. Their proximity immediately leads us to compare them and to decide that the rock on the left is larger than the rock on the right. Figure 2.3 shows the rock on the right in its natural setting. Now we can see that it is actually a very large rock. The hand on the rock gives a very good reference from which to judge its size. Like the rock in the hand, the rock with the hand on top provides us with a scale that permits a relative determination of size. It is clear from these simple illustrations that under normal circumstances, we take size to be relative. We know how big something is by comparing it to something else.

FIGURE 2.2. The rock from Figure 2.1 in a hand.

FIGURE 2.3. The other rock from Figure 2.1, but now in a context from which its size can be judged.

OBSERVATION METHOD CAN MATTER

Why does the definition of size, relative versus absolute, matter? To observe something, we must interact with it. This is true in both classical and quantum mechanics.

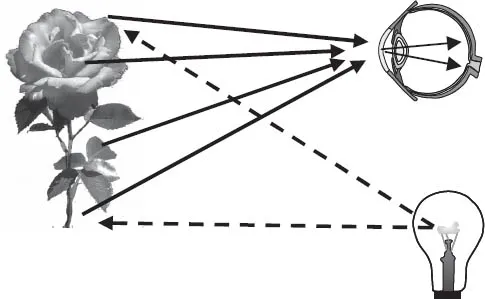
Figure 2.4 illustrates the observation of a rose. In a totally dark room, we cannot see the rose. In Figure 2.4, however, light emanating from the light bulb falls on the rose. Some of the light is absorbed, and some of it bounces off. (Which colors are absorbed, and therefore, which colors bounce off to make the leaves look green and the petals look red, is a strictly quantum mechanical phenomenon that will be discussed in Chapter 8.) A portion of the light that bounces off is detected by the eye and processed by the brain to observe the rose. The observer is interacting with the rose through the light that bounces off it.

FIGURE 2.4. The light bulb illuminates the rose. The light that bounces off the rose enters the eye, enabling us to see the rose.

Once we recognize that we must interact with an object to observe it, we are in a position to define big and small. The definition of what is big and what is small is identical in classical mechanics and quantum mechanics. If the disturbance to an obj...

Table of contents

• Cover Page
• Title Page
• Copyright Page
• Contents
• Preface
• Chapter 1 Schrödinger’s Cat
• Chapter 2 Size Is Absolute
• Chapter 3 Some Things About Waves
• Chapter 4 The Photoelectric Effect and Einstein’s Explanation
• Chapter 5 Light: Waves or Particles?
• Chapter 6 How Big Is a Photon and the Heisenberg Uncertainty Principle
• Chapter 7 Photons, Electrons, and Baseballs
• Chapter 8 Quantum Racquetball and the Color of Fruit
• Chapter 9 The Hydrogen Atom: The History
• Chapter 10 The Hydrogen Atom: Quantum Theory
• Chapter 11 Many Electron Atoms and the Periodic Table of Elements
• Chapter 12 The Hydrogen Molecule and the Covalent Bond
• Chapter 13 What Holds Atoms Together: Diatomic Molecules
• Chapter 14 Bigger Molecules: The Shapes of Polyatomic Molecules
• Chapter 15 Beer and Soap
• Chapter 16 Fat, It’s All About the Double Bonds
• Chapter 17 Greenhouse Gases
• Chapter 18 Aromatic Molecules
• Chapter 19 Metals, Insulators, and Semiconductors
• Chapter 20 Think Quantum
• Glossary
• Index