
- 712 pages
- English
- ePUB (mobile friendly)
- Available on iOS & Android
Econometrics
About this book
The most authoritative and comprehensive synthesis of modern econometrics available
Econometrics provides first-year graduate students with a thoroughly modern introduction to the subject, covering all the standard material necessary for understanding the principal techniques of econometrics, from ordinary least squares through cointegration. The book is distinctive in developing both time-series and cross-section analysis fully, giving readers a unified framework for understanding and integrating results.
Econometrics covers all the important topics in a succinct manner. All the estimation techniques that could possibly be taught in a first-year graduate course, except maximum likelihood, are treated as special cases of GMM (generalized methods of moments). Maximum likelihood estimators for a variety of models, such as probit and tobit, are collected in a separate chapter. This arrangement enables students to learn various estimation techniques in an efficient way. Virtually all the chapters include empirical applications drawn from labor economics, industrial organization, domestic and international finance, and macroeconomics. These empirical exercises provide students with hands-on experience applying the techniques covered. The exposition is rigorous yet accessible, requiring a working knowledge of very basic linear algebra and probability theory. All the results are stated as propositions so that students can see the points of the discussion and also the conditions under which those results hold. Most propositions are proved in the text.
For students who intend to write a thesis on applied topics, the empirical applications in Econometrics are an excellent way to learn how to conduct empirical research. For theoretically inclined students, the no-compromise treatment of basic techniques is an ideal preparation for more advanced theory courses.
Frequently asked questions
- Essential is ideal for learners and professionals who enjoy exploring a wide range of subjects. Access the Essential Library with 800,000+ trusted titles and best-sellers across business, personal growth, and the humanities. Includes unlimited reading time and Standard Read Aloud voice.
- Complete: Perfect for advanced learners and researchers needing full, unrestricted access. Unlock 1.4M+ books across hundreds of subjects, including academic and specialized titles. The Complete Plan also includes advanced features like Premium Read Aloud and Research Assistant.
Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app.
Information
CHAPTER 1
Finite-Sample Properties of OLS
ABSTRACT
1.1 The Classical Linear Regression Model
The Linearity Assumption
Assumption 1.1 (linearity):
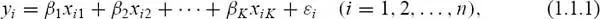
Table of contents
- Cover
- Half title
- Title
- Copyright
- Contents
- List of Figures
- Preface
- 1 Finite-Sample Properties of OLS
- 2 Large-Sample Theory
- 3 Single-Equation GMM
- 4 Multiple-Equation GMM
- 5 Panel Data
- 6 Serial Correlation
- 7 Extremum Estimators
- 8 Examples of Maximum Likelihood
- 9 Unit-Root Econometrics
- 10 Cointegration
- Appendix A: Partitioned Matrices and Kronecker Products
- Index