Quantum Mechanics in a Nutshell

Gerald D. Mahan

• Publisher: Princeton University Press
• Year: 2008
• Print ISBN: 9780691137131
• eBook ISBN: 9781400833382
• Topic: Physical Sciences
• Subtopic: Condensed Matter

Covering the fundamentals as well as many special topics of current interest, this is the most concise, up-to-date, and accessible graduate-level textbook on quantum mechanics available. Written by Gerald Mahan, a distinguished research physicist and author of an acclaimed textbook on many-particle physics, Quantum Mechanics in a Nutshell is the distillation of many years' teaching experience.


Emphasizing the use of quantum mechanics to describe actual quantum systems such as atoms and solids, and rich with interesting applications, the book proceeds from solving for the properties of a single particle in potential; to solving for two particles (the helium atom); to addressing many-particle systems. Applications include electron gas, magnetism, and Bose-Einstein Condensation; examples are carefully chosen and worked; and each chapter has numerous homework problems, many of them original.



Quantum Mechanics in a Nutshell expertly addresses traditional and modern topics, including perturbation theory, WKBJ, variational methods, angular momentum, the Dirac equation, many-particle wave functions, Casimir Force, and Bell's Theorem. And it treats many topics--such as the interactions between photons and electrons, scattering theory, and density functional theory--in exceptional depth.


A valuable addition to the teaching literature, Quantum Mechanics in a Nutshell is ideally suited for a two-semester course.

• The most concise, up-to-date, and accessible graduate textbook on the subject


• Contains the ideal amount of material for a two-semester course


• Focuses on the description of actual quantum systems, including a range of applications


• Covers traditional topics, as well as those at the frontiers of research


• Treats in unprecedented detail topics such as photon-electron interaction, scattering theory, and density functional theory


• Includes numerous homework problems at the end of each chapter

1 Introduction

1.1 Introduction

Quantum mechanics is a mathematical description of how elementary particles move and interact in nature. It is based on the wave–particle dual description formulated by Bohr, Einstein, Heisenberg, Schrödinger, and others. The basic units of nature are indeed particles, but the description of their motion involves wave mechanics.

The important parameter in quantum mechanics is Planck’s constant h = 6.626 × 10⁻³⁴ J s. It is common to divide it by 2π, and to put a slash through the symbol: ħ = 1.054 × 10⁻³⁴ J s. Classical physics treated electromagnetic radiation as waves. It is particles, called photons, whose quantum of energy is ħω where ω is the classical angular frequency. For particles with a mass, such as an electron, the classical momentum

, where the wave vector k gives the wavelength k = 2π/λ of the particle. Every particle is actually a wave, and some waves are actually particles.

The wave function

(r, t) is the fundamental function for a single particle. The position of the particle at any time t is described by the function |

(r, t)|², which is the probability that the particle is at position r at time t. The probability is normalized to one by integrating over all positions:

In classical mechanics, it is assumed that one can know exactly where a particle is located. Classical mechanics takes this probability to be

The three-dimensional delta-function has an argument that includes the particle velocity v. In quantum mechanics, we never know precisely where to locate a particle. There is always an uncertainty in the position, the momentum, or both. This uncertainty can be summarized by the Heisenberg uncertainty principle:

Table 1.1 Fundamental Constants and Derived Quantities

where Δx is the uncertainty in position along one axis, Δp_x is the uncertainty in momentum along the same axis, and ħ is Planck’s constant h divided by 2π(ħ = h/2π), and has the value ħ = 1.05 × 10⁻³⁴ joules-second. Table 1.1 lists some fundamental constants.

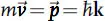
1.2 Schrödinger’s Equation

The exact form of the wave function

(r, t) depends on the kind of particle, and its environment. Schrödinger’s equation is the fundamental nonrelativistic equation used in quantum mechanics for describing microscopic particle motions. For a system of particles, Schrödinger’s equation is written as

The particles have positions r_i, momentum p_j, and spin s_j. They interact with a potential U(r_j, s_j) and with each other through the pair interaction V(r_i − r_j). The quantity H is the Hamiltonian, and the wave function for a system of many particles is

.

The specific forms for H depends on the particular problem. The relativistic form of the Hamiltonian is different than the nonrelativistic one. The relativistic Hamiltonian is discussed in chapter 11. The Hamiltonian can be used to treat a single particle, a collection of identical particles, or different kinds of elementary particles. Many-particle systems are solved in chapter 9.

No effort is made here to justify the correctness of Schrödinger’s equation. It is assumed that the student has had an earlier course in the introduction to modern physics and quantum mechanics. A fundamental equation such as eqn. (1.4) cannot be derived from any postulate-free starting point. The only justification for its correctness is that its predictions agree with experiment. The object of this textbook is to teach the student how to solve Schrödinger’s equation and to make these predictions. The students will be able to provide their own comparisons to experiment.

Schrödinger’s equation for a single nonrelativistic particle of mass m, in the ab...

Table of contents

• Cover
• Half title
• Title
• Copyright
• Contents
• Preface
• 1 Introduction
• 2 One Dimension
• 3 Approximate Methods
• 4 Spin and Angular Momentum
• 5 Two and Three Dimensions
• 6 Matrix Methods and Perturbation Theory
• 7 Time-Dependent Perturbations
• 8 Electromagnetic Radiation
• 9 Many-Particle Systems
• 10 Scattering Theory
• 11 Relativistic Quantum Mechanics
• Index