e: The Story of a Number

Eli Maor

• Publisher: Princeton University Press
• Year: 2011
• Print ISBN: 9780691058542, 9780691033907
• eBook ISBN: 9781400832347
• Topic: Mathematics
• Subtopic: History & Philosophy of Mathematics
• Index: Mathematics

The interest earned on a bank account, the arrangement of seeds in a sunflower, and the shape of the Gateway Arch in St. Louis are all intimately connected with the mysterious number e. In this informal and engaging history, Eli Maor portrays the curious characters and the elegant mathematics that lie behind the number. Designed for a reader with only a modest mathematical background, this biography brings out the central importance of e to mathematics and illuminates a golden era in the age of science.

1

John Napier, 1614

Seeing there is nothing that is so troublesome to mathematical practice, nor that doth more molest and hinder calculators, than the multiplications, divisions, square and cubical extractions of great numbers…. I began therefore to consider in my mind by what certain and ready art I might remove those hindrances.
—JOHN NAPIER, Mirifici logarithmorum canonis descriptio (1614)¹

Rarely in the history of science has an abstract mathematical idea been received more enthusiastically by the entire scientific community than the invention of logarithms. And one can hardly imagine a less likely person to have made that invention. His name was John Napier.²

The son of Sir Archibald Napier and his first wife, Janet Bothwell, John was born in 1550 (the exact date is unknown) at his family’s estate, Merchiston Castle, near Edinburgh, Scotland. Details of his early life are sketchy. At the age of thirteen he was sent to the University of St. Andrews, where he studied religion. After a sojourn abroad he returned to his homeland in 1571 and married Elizabeth Stirling, with whom he had two children. Following his wife’s death in 1579, he married Agnes Chisholm, and they had ten more children. The second son from this marriage, Robert, would later be his father’s literary executor. After the death of Sir Archibald in 1608, John returned to Merchiston, where, as the eighth laird of the castle, he spent the rest of his life.³

Napier’s early pursuits hardly hinted at future mathematical creativity. His main interests were in religion, or rather in religious activism. A fervent Protestant and staunch opponent of the papacy, he published his views in A Plaine Discovery of the whole Revelation of Saint John (1593), a book in which he bitterly attacked the Catholic church, claiming that the pope was the Antichrist and urging the Scottish king James VI (later to become King James I of England) to purge his house and court of all “Papists, Atheists, and Newtrals.”⁴ He also predicted that the Day of Judgment would fall between 1688 and 1700. The book was translated into several languages and ran through twenty-one editions (ten of which appeared during his lifetime), making Napier confident that his name in history—or what little of it might be left—was secured.

Napier’s interests, however, were not confined to religion. As a landowner concerned to improve his crops and cattle, he experimented with various manures and salts to fertilize the soil. In 1579 he invented a hydraulic screw for controlling the water level in coal pits. He also showed a keen interest in military affairs, no doubt being caught up in the general fear that King Philip II of Spain was about to invade England. He devised plans for building huge mirrors that could set enemy ships ablaze, reminiscent of Archimedes’ plans for the defense of Syracuse eighteen hundred years earlier. He envisioned an artillery piece that could “clear a field of four miles circumference of all living creatures exceeding a foot of height,” a chariot with “a moving mouth of mettle” that would “scatter destruction on all sides,” and even a device for “sayling under water, with divers and other stratagems for harming of the enemyes”—all forerunners of modern military technology.⁵ It is not known whether any of these machines was actually built.

As often happens with men of such diverse interests, Napier became the subject of many stories. He seems to have been a quarrelsome type, often becoming involved in disputes with his neighbors and tenants. According to one story, Napier became irritated by a neighbor’s pigeons, which descended on his property and ate his grain. Warned by Napier that if he would not stop the pigeons they would be caught, the neighbor contemptuously ignored the advice, saying that Napier was free to catch the pigeons if he wanted. The next day the neighbor found his pigeons lying half-dead on Napier’s lawn. Napier had simply soaked his grain with a strong spirit so that the birds became drunk and could barely move. According to another story, Napier believed that one of his servants was stealing some of his belongings. He announced that his black rooster would identify the transgressor. The servants were ordered into a dark room, where each was asked to pat the rooster on its back. Unknown to the servants, Napier had coated the bird with a layer of lampblack. On leaving the room, each servant was asked to show his hands; the guilty servant, fearing to touch the rooster, turned out to have clean hands, thus betraying his guilt.⁶

All these activities, including Napier’s fervent religious campaigns, have long since been forgotten. If Napier’s name is secure in history, it is not because of his best-selling book or his mechanical ingenuity but because of an abstract mathematical idea that took him twenty years to develop: logarithms.

The sixteenth and early seventeenth centuries saw an enormous expansion of scientific knowledge in every field. Geography, physics, and astronomy, freed at last from ancient dogmas, rapidly changed man’s perception of the universe. Copernicus’s heliocentric system, after struggling for nearly a century against the dictums of the Church, finally began to find acceptance. Magellan’s circumnavigation of the globe in 1521 heralded a new era of marine exploration that left hardly a corner of the world unvisited. In 1569 Gerhard Mercator published his celebrated new world map, an event that had a decisive impact on the art of navigation. In Italy Galileo Galilei was laying the foundations of the science of mechanics, and in Germany Johannes Kepler formulated his three laws of planetary motion, freeing astronomy once and for all from the geocentric universe of the Greeks. These developments involved an ever increasing amount of numerical data, forcing scientists to spend much of their time doing tedious numerical computations. The times called for an invention that would free scientists once and for all from this burden. Napier took up the challenge.

We have no account of how Napier first stumbled upon the idea that would ultimately result in his invention. He was well versed in trigonometry and no doubt was familiar with the formula

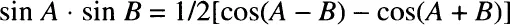
This formula, and similar ones for cos A · cos B and sin A · cos B, were known as the prosthaphaeretic rules, from the Greek word meaning “addition and subtraction.” Their importance lay in the fact that the product of two trigonometric expressions such as sin A · sin B could be computed by finding the sum or difference of other trigonometric expressions, in this case cos(A − B) and cos(A + B). Since it is easier to add and subtract than to multiply and divide, these formulas provide a primitive system of reduction from one arithmetic operation to another, simpler one. It was probably this idea that put Napier on the right track.

A second, more straightforward idea involved the terms of a geometric progression, a sequence of numbers with a fixed ratio between successive terms. For example, the sequence 1, 2, 4, 8, 16, … is a geometric progression with the common ratio 2. If we denote the common ratio by q, then, starting with 1, the terms of the progression are 1, q, q², q³, and so on (note that the nth term is qⁿ⁻¹). Long before Napier’s time, it had been noticed that there exists a simple relation between the terms of a geometric progression and the corresponding exponents, or indices, of the common ratio. The German mathematician Michael Stifel (1487–1567), in his book Arithmetica integra (1544), formulated this relation as follows: if we multiply any two terms of the progression 1, q, q², …, the result would be the same as if we had added the corresponding exponents.⁷ For example, q² · q³ = (q · q) · (q · q · q) = q · q · q · q · q = q⁵, a result that could have been obtained by adding the exponents 2 and 3. Similarly, dividing one term of a geometric progression by another term is equivalent to subtracting their exponents: q⁵/q³ = (q · q...

Table of contents

• Cover Page
• Title Page
• Copyright Page
• Dedication Page
• Contents
• Preface
• 1. John Napier, 1614
• 2. Recognition
• 3. Financial Matters
• 4. To the Limit, If It Exists
• 5. Forefathers of the Calculus
• 6. Prelude to Breakthrough
• 7. Squaring the Hyperbola
• 8. The Birth of a New Science
• 9. The Great Controversy
• 10. ex: The Function That Equals Its Own Derivative
• 11. eθ: Spira Mirabilis
• 12. (ex + e−x)/2: The Hanging Chain
• 13. eix: “The Most Famous of All Formulas”
• 14. ex+iy: The Imaginary Becomes Real
• 15. But What Kind of Number Is It?
• Appendixes
• Bibliography
• Index